| > |
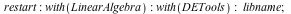 |
 |
(1) |
| > |
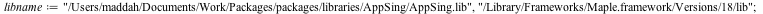 |
 |
(2) |
| > |
 |
Desingp(Matrix,variable,p) tests and performs desingularization at an irreducible polynomial p
Desing(Matrix,variable) identifies, tests, and performs desingularization at all irreducible polynomials p
The output is the change of basis T, its inverse invT, the matrix B of the equivalent desingularized system, and the execution time t, respectively.
DesingpSteps(Matrix,variable,p) and DesingSteps(Matrix,variable) give the same output and print key intermediate steps as well
For more information, please refer to our paper entitled "Removing Apparent Singularities of Systems of Linear Differential Equations with Rational Function Coefficients" and/or the description of the package.
Example 1 (Example 1 in the paper)
Input Matrix
| > |
![A := Matrix(2, 2, [0, 1, `/`(`*`(`+`(`*`(4, `*`(`^`(z, 2))), `-`(2))), `*`(`+`(`*`(`^`(z, 2)), 2))), `+`(`-`(`/`(`*`(`+`(`*`(3, `*`(`^`(z, 2))), `-`(4))), `*`(z, `*`(`+`(`*`(`^`(z, 2)), 2))))))]); 1](images/AppSing_examples_presentation_13.gif) |
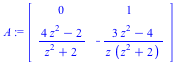 |
(1.1.1) |
Desingularization at p= z^2 +2
| > |
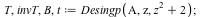 |
 |
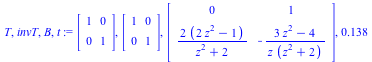 |
(1.2.1) |
Details of Desingularization at p= z^2 +2 ( intermediate steps)
| > |
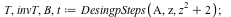 |
Desingularization at p= z
| > |
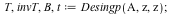 |
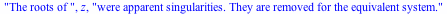 |
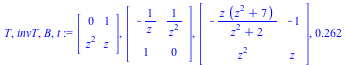 |
(1.4.1) |
Details of Desingularization at p= z ( intermediate steps)
| > |
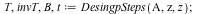 |
Desingularization
| > |
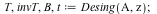 |
Details of Desingularization
| > |
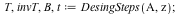 |
Example 2: Shaoshi Chen, M. Jaroschek, M. Kauers, M. F.Singer, Desingularization Explains Order-Degree Curves for Ore Operators, Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, pp. 157-164, ACM, U.S.A. (2013))
Input Matrix
| > |
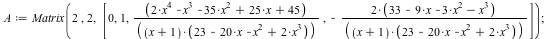 |
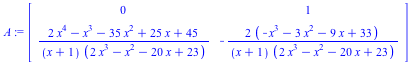 |
(2.1.1) |
Desingularization at p= 2*x^3 -x^2 -20*x +23
| > |
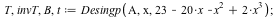 |
| > |
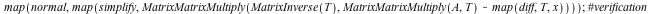 |
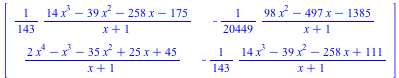 |
(2.2.2) |
Details of Desingularization at p= 2*x^3 -x^2 -20*x +23 (intermediate steps)
| > |
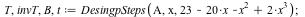 |
Example 3 (the introductory example in the paper)
Input Matrix
| > |
![A := Matrix(2, 2, [0, 1, `+`(`-`(`/`(`*`(2), `*`(z)))), `+`(1, `/`(`*`(2), `*`(z)))]); 1](images/AppSing_examples_presentation_55.gif) |
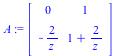 |
(3.1.1) |
Desingularization
| > |
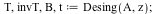 |
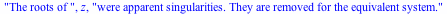 |
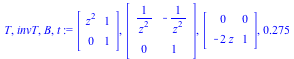 |
(3.2.1) |
Example 4: Shaoshi Chen, M. Kauers, M. F. Singer, Desingularization of Ore Operators, Available at: arXiv:1408.5512v1, (2014))
Input Matrix
| > |
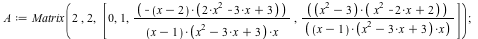 |
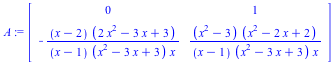 |
(4.1.1) |
Desingularization at p = x^2 - 3*x +3
| > |
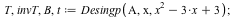 |
 |
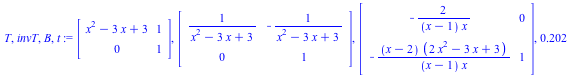 |
(4.2.1) |
Desingularization
| > |
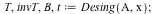 |
Example 5: A. Bostan, S. Boukraa, S. Hassani, M. van Hoeij, J.-M. Maillard, J.-A. Weil, and N. Zenine, The Ising model: From Elliptic Curves to ModularForms and Calabi-Yau equations. J. Phys. A: Math. Theor., 44(4):045204, 44, (2011))
Example 5.2 : DE from http://www.unilim.fr/pages_perso/jacques-arthur.weil/L3tilde.mpl
Input Matrix
Desingularization at 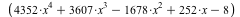
| > |
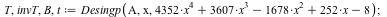 |
Desingularization
| > |
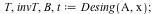 |
Example 5.2 : DE from http://www.ms.unimelb.edu.au/~iwan/ising/series/Chi5/L11.txt
DE
Input Matrix
| > |
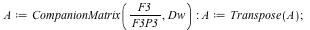 |
| > |
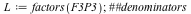 |
Desingularization at p(w) (of degree 37)
Desingularization
| > |
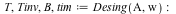 |
| > |
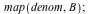 |
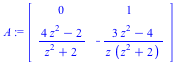
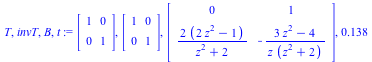
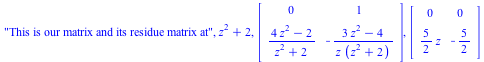
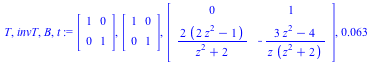
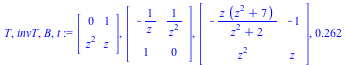
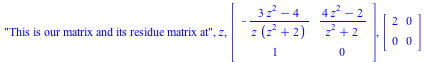
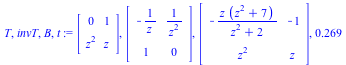
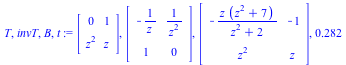
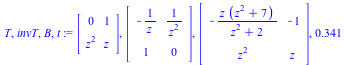
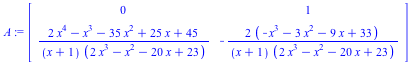
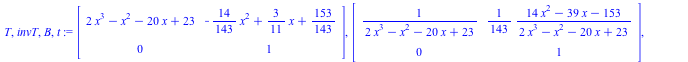
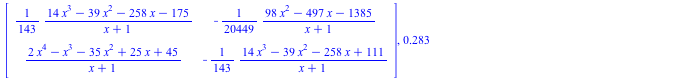
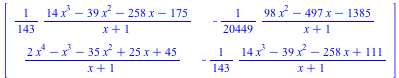
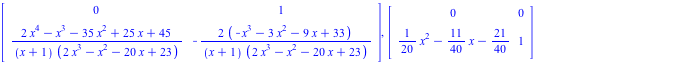
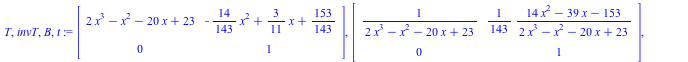
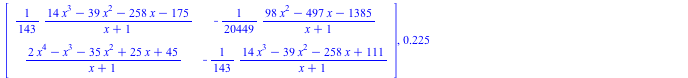
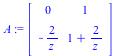
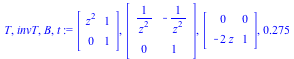
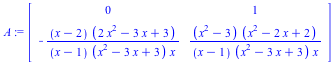
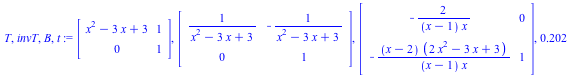
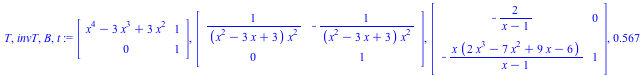
![]()