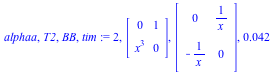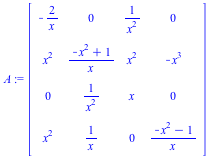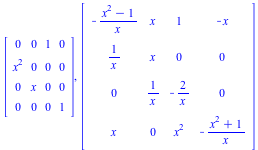| > |
 |
 |
(1) |
| > |
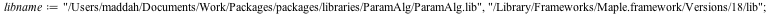 |
 |
(2) |
| > |
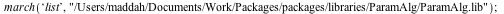 |
Given a one-parameter perturbation A(x) of a constant matrix, this package offers functions to recover leading terms and orders (or their bounds) of its eigenvalues from a few low order coefficients of a matrix similar to A(x). For more info, please refer to Chapter 2 of my thesis or to the following articles:
- Jeannerod, C-P., and Eckhard Pflügel. "A reduction algorithm for matrices depending on a parameter." Proceedings of the 1999 international symposium on Symbolic and algebraic computation. ACM, 1999.
- Jeannerod, Claude-Pierre. "An algorithm for the eigenvalue perturbation problem: reduction of a κ-matrix to a Lidskii matrix." Proceedings of the 2000 international symposium on Symbolic and algebraic computation. ACM, 2000.
AlgMoser(A,x,truncation) computes a transformation T(x) such that B = T^{-1} A T is in CRV form (has both a maximal valuation v and a minimal number of nonzero volumns of valuation v).
AlgTurnPt1(A,x,truncation) where A(x) is a non-nilpotent matrix, makes use of AlgMoser to compute a transformation T1(x), an integer s (computed using the Newton polygon associated to the characteristic polynomial), and a transformation T2(x), such that applying T1(x), the ramification x =t^s, and T2(x), yields a matrix B(x) whose leading coefficient is not nilpotent (i.e. the coefficient of lowest order).
AlgTurnPt2(A,x,truncation) computes s and a transformation T(x) for the same purpose as above. In other words, it takes T1(x) to be the identity matrix and T2(x) to be T(x).
| > |
![A := Matrix(2, 2, [0, 1, `*`(`^`(x, 5)), 0]); 1; Eigenvalues(A); 1; AlgTurnPt1(A, x, 10); 1; AlgTurnPt2(A, x, 10); 1](images/ParamAlg_examples_10.gif) |
| > |
![A := Matrix(3, 3, [0, 1, 0, 0, 0, 1, 0, 0, x]); 1; Eigenvalues(A); 1; AlgTurnPt1(A, x, 10); 1](images/ParamAlg_examples_15.gif) |
| > |
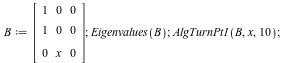 |
| > |
![A := Matrix(2, 2, [0, 1, `*`(`^`(x, 5)), 0]); 1; Eigenvalues(A); 1; AlgTurnPt1(A, x, 10); 1](images/ParamAlg_examples_23.gif) |
| > |
 |
| > |
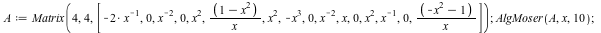 |
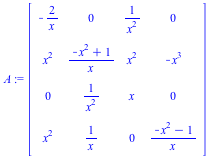 |
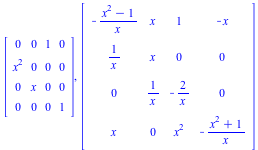 |
(9) |
| > |
![A := Matrix(2, 2, [0, 1, `*`(`^`(x, 5)), 0]); 1; AlgMoser(A, x, 10); 1](images/ParamAlg_examples_34.gif) |
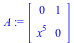 |
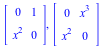 |
(10) |
| > |
![A := Matrix(2, 2, [0, 1, `*`(`^`(x, 2)), 0]); 1; s, T, B, t := AlgTurnPt1(A, x, 10); 1](images/ParamAlg_examples_37.gif) |
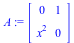 |
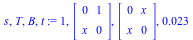 |
(11) |
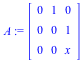
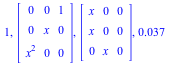
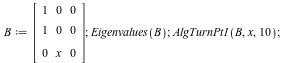
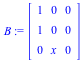
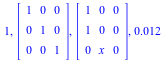

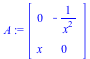
](images/ParamAlg_examples_29.gif)