Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

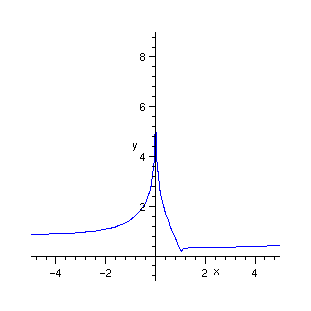
On peut se demander s'il est nécessaire de disposer d'un outil aussi puissant que Maple pour étudier la fonction proposée. Il est clair qu'elle est définie pour tout réel non nul et qu'elle est indéfiniment dérivable en tout point de son ensemble de définition différent de 1. En 0 le terme dominant est le logarithme et le graphe possède une asymptote verticale. À l'infini c'est la racine carrée qui dicte le comportement de la fonction et le graphe a une branche parabolique.

Le logiciel n'est utile que pour la recherche des points critiques. Pour l'employer il faut définir une expression qui représente la fonction.

> f:=sqrt(abs(x-1))-ln(abs(x));

À partir de V.4, il devient possible d'employer un objet de type piecewise.

> F:=convert(f,piecewise);

On pourrait aussi définir une expression par intervalle utile, de manière à se débarasser des valeurs absolues, peu appréciées d'un système de calcul formel. Cette façon de faire fonctionne dans toutes les versions.

> op(F);

> for i to 3 do f.i:=op(2*i,F) od;

Nous déterminons les points critiques, c'est-à-dire les points qui annulent la dérivée.

> F1:=diff(F,x);

> critical:=[solve(F1,x)];

Ici Maple V.3 ne trouve que le point 2. Pour étudier les points critiques, on peut calculer les dérivées successives de la fonction et leur valeurs en ces points. Il est plus efficace d'employer series. On notera l'utilisation de radnormal qui existe depuis V.4.

> series(f,x=critical[1]);

> map(radnormal,%);

> series(f,x=critical[2]);

On voit que 2 fournit un point d'inflexion alors que l'autre point critique correspond à un minimum local. Pour finir nous traçons le graphique.

> plot(f,x=-5..5,y=-1..9,color=blue);

Retour en page principale