Calcul formel : Mode d'emploi - Exemples en Maple
Claude Gomez, Bruno Salvy, Paul Zimmermann
Masson, 1995
Chapitre II, section 3.4, exercice 3, page 74.
Philippe.Dumas@inria.fr
http://algo.inria.fr/dumas/Maple/
|
|
Minimum vital | Amélioration de l'évaluation numérique | Multiséries
Minimum vital. Dans la mesure où nous voulons intégrer une nouvelle fonction au système, il faut commencer par définir une procédure qui représente la fonction. On doit donc se poser la question de savoir où est définie la fonction que l'on veut représenter par la procédure invGAMMA. Il est clair que c'est une difficulté de l'exercice. On peut envisager divers points de vue. Le plus simple est de considérer la fonction GAMMA dans le domaine réel pour des arguments plus grands que 2. C'est ce que nous ferons. On pourrait aussi vouloir travailler avec des réels quelconques, mais il faut alors faire des choix car on n'a plus affaire à une injection. En fait, dès qu'on sort du cas simple que nous voulons considérer, on est amené à travailler dans l'optique des fonctions holomorphes et à définir des branches. La difficulté est alors de faire les choix des domaines pour les différentes branches et de mettre au point des procédures de calcul numérique dignes de ce nom. On pourrait s'inspirer du traitement de la fonction W, dite de Lambert, mais ici le problème est encore plus délicat car les points critiques ne sont pas exactement connus (il faudrait les traiter symboliquement).
Nous considérons donc que GAMMA^(-1) est définie entre 1 et l'infini positif. Elle est la fonction réciproque de la fonction GAMMA restreinte aux réels entre 2 et l'infini positif.
La procédure invGAMMA traite d'abord le cas d'une factorielle, au sens formel c'est-à-dire écrite avec un point d'exclamation (#1). Ensuite on considère le cas des entiers strictement positifs (#2) ; la procédure repère les entiers qui sont des factorielles, au sens numérique, en s'appuyant sur une procédure d'évaluation numérique evalf/invGAMMA, qui n'est pas encore écrite. Le cas de l'entier 1, qui est vu comme l'image de 2, d'après le choix qui a été fait, demande d'être traité à part. Pour éviter des tests, nous employons une table de remember comme on le voit après le end de la procédure (#6). Après quoi, les images des demi-entiers par GAMMA sont traitées ; pour tous les demi-entiers plus grands que 2, l'image par GAMMA s'écrit r*Pi^(1/2) où r est un rationnel strictement plus grand que 1, sauf pour le demi-entier 5/2. Pour éviter de compliquer le code, nous employons ici encore la table de remember. On notera que les images des demi-entiers 1/2 et 3/2 ne sont pas rejetées ; la valeur de invGAMMA sur ces deux arguments n'est simplement pas évaluée. On pourrait provoquer une erreur, cependant on sait bien que cette version n'est pas réaliste et qu'il faudrait étendre cet inverse, donc on préfère laisser la question en attente. On passe ensuite aux flottants (#4) en appelant la procédure d'évaluation numérique. Si aucun des cas précédents n'a été rencontré, on renvoie l'expression non évaluée (#5). Notons que l'efficacité du code pourrait être améliorée dans le cas des entiers positifs et des multiples de Pi^(1/2).
> invGAMMA:=proc(x::algebraic)
local z,f,n;
if type(x,`!`) then op(1,x)+1 #1
elif type(x,posint) then #2
z:=`evalf/invGAMMA`(x);
f:=1;
for n from 2 to z do
f:=n*f;
if f=x then RETURN(n+1) fi
od;
'invGAMMA(x)'
elif type(x/Pi^(1/2),rational) and x/Pi^(1/2)>1 then #3
z:=`evalf/invGAMMA`(x);
f:=1/2;
for n from 2 to z do
f:=(n-1/2)*f;
if f=x/Pi^(1/2) then RETURN(n+1/2) fi
od;
'invGAMMA(x)'
elif type(x,float) then #4
`evalf/invGAMMA`(x)
else
'invGAMMA'(x) #5
fi
end:
invGAMMA(1):=2: #6
invGAMMA(3/4*Pi^(1/2)):=5/2:
Nous avons besoin d'une procédure d'évaluation numérique. Nous nous contentons de tester l'argument et d'appeler fsolve.
> `evalf/invGAMMA`:=proc(x::algebraic)
local xx;
xx:=evalf(x);
if xx>=1 then
fsolve(GAMMA(t)=xx,t=2..infinity)
else
ERROR("evalf/invGAMMA expects its argument to be
not smaller than 1, but received ",x)
fi
end:
Nous pouvons maintenant effectuer quelques tests.
> seq(invGAMMA(n),n=1..6);
![]()
> invGAMMA(N!);
![]()
> seq(invGAMMA(GAMMA(n+1/2)),n=2..5);
![]()
> evalf(invGAMMA(10));
![]()
> invGAMMA(10.);
![]()
Les résultats sont corrects, mais l'exécution est un peu lente parce que la procédure d'évaluation numérique n'est pas assez efficace. Nous reviendrons plus loin sur ce point.
Ce qui précède est notoirement insuffisant pour que la fonction GAMMA^(-1) soit intégrée au système. En effet nous n'avons encore rien qui exprime la relation fondamentale GAMMA(GAMMA^(-1)(x))=x.
> GAMMA(invGAMMA(x));
![]()
Il faut donc absolument introduire cette simplification attendue, sinon la procédure invGAMMA ne représente pas un inverse fonctionnel de GAMMA. Pour cela il faudrait modifier la procédure simplify/GAMMA, ou plutôt la procédure simplify/GAMMA/combine qui est appelée par la précédente.
> subsop(3=NULL,readlib(`simplify/GAMMA`));
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cependant il n'est pas question d'aller modifier le système. Il doit rester dans sa forme officielle pour que l'utilisateur puisse communiquer avec d'autres utilisateurs. Nous allons donc nous contenter d'une modification qui ne sera pas vraiment intégrée au système puisqu'il faudra appeler explicitement la procédure que nous allons écrire. Le code de cette procédure mysimplify/GAMMA est directement inspirée du code de simplify/GAMMA/combine.
> `mysimplify/GAMMA`:=proc(f)
local g,h;
if type(f,{table, procedure, name, numeric}) then f
elif not has(f,{GAMMA,invGAMMA}) then f
else
g:=readlib(`simplify/GAMMA`)(f);
if type(g,function) and op(0,g)=GAMMA then
h:=op(1,g);
if type(h,function) and op(0,h)=invGAMMA then
op(1,h)
else g
fi
else
map(procname,g)
fi
fi
end:
Cette procédure exprime que invGAMMA représente un inverse fonctionnel pour la fonction GAMMA.
> `mysimplify/GAMMA`(GAMMA(invGAMMA(x)));
![]()
Si l'on met en parallèle la fonction GAMMA et
l'élévation au carré, on peut dire que nous avons
maintenant l'équivalent de la formule
![]() . Mais voulons nous aussi disposer de la formule
. Mais voulons nous aussi disposer de la formule
![]() ? Cela se discute. Jusqu'à la version V.3 de Maple,
des récritures de ce type était effectuées
par simplify (par exemple pour ln(exp(x))). À
partir de la version V.4, elles sont effectuées avec un
simplify qui comporte l'option
symbolic. L'idée sous-jacente est que les
indéterminées représentent des nombres
complexes. Ce que nous avons écrit jusqu'ici ne produit aucune
simplification de cette sorte.
? Cela se discute. Jusqu'à la version V.3 de Maple,
des récritures de ce type était effectuées
par simplify (par exemple pour ln(exp(x))). À
partir de la version V.4, elles sont effectuées avec un
simplify qui comporte l'option
symbolic. L'idée sous-jacente est que les
indéterminées représentent des nombres
complexes. Ce que nous avons écrit jusqu'ici ne produit aucune
simplification de cette sorte.
> invGAMMA(GAMMA(x));
![]()
> `mysimplify/GAMMA`(invGAMMA(GAMMA(x)));
![]()
Pour introduire cette simplification, nous allons ajouter une procédure mysimplify/GAMMA/symbolic.
> `mysimplify/GAMMA/symbolic`:=proc(f)
local g,h;
if type(f,{table, procedure, name, numeric}) then f
elif not has(f,{GAMMA,invGAMMA}) then f
else
g:=readlib(`simplify/GAMMA`)(f);
if type(g,function) then
h:=op(1,g);
if type(h,function) then
if {op(0,g),op(0,h)}={GAMMA,invGAMMA} then
op(1,h)
else g
fi
fi
else
map(procname,g)
fi
fi
end:
Nous avons ainsi la simplification annoncée. C'est à l'utilisateur de savoir s'il veut employer cette récriture.
> `mysimplify/GAMMA/symbolic`(GAMMA(invGAMMA(x)));
![]()
> `mysimplify/GAMMA/symbolic`(invGAMMA(GAMMA(x)));
![]()
> `mysimplify/GAMMA/symbolic`(invGAMMA(x*GAMMA(x)));
![]()
Ce qui précède est encore insuffisant pour que la fonction GAMMA^(-1) soit intégrée au système. Il faut, pour chaque opération qu'il est raisonnable d'appliquer à cette fonction, modifier la procédure correspondante pour qu'elle prenne en compte la procédure invGAMMA. Par exemple, il faut spécifier l'action de la dérivation. Dans ce cas, le code à écrire est facile parce que le logiciel comprend un mécanisme simple d'extension. Il suffit d'écrire une procédure diff/invGAMMA. Elle sera appelée par diff et doit fournir la dérivée de GAMMA^(-1)(a(x)) par rapport à x. La relation GAMMA'(x)/GAMMA(x)=Psi(x) donne tout de suite la formule à employer.
> `diff/invGAMMA`:=proc(a,x)
1/a/Psi(invGAMMA(a))*diff(a,x)
end:
> diff(invGAMMA(t*exp(t)),t);
![[Maple Math]](images/ex3_25.gif)
Le cas de l'intégration est plus compliqué à mettre en oeuvre. Là aussi, on pourrait introduire une procédure int/invGAMMA. Bref la question est loin d'être traitée dans son entier et l'on voit que l'introduction d'une nouvelle fonction mathématique dans le système est un travail de longue haleine. Tout cela est bien décrit au paragraphe 3.3, pp. 69-72. En particulier la table II.5 de la page 72 donne les procédures extensibles.
Amélioration de l'évaluation numérique. Nous voulons récrire la procédure evalf/invGAMMA pour qu'elle soit plus efficace. L'idée est la suivante : nous allons d'abord trouver une assez bonne approximation de la valeur de GAMMA^(-1)(x) puis, à partir de cette approximation, nous appliquerons la méthode de Newton à l'équation GAMMA(z)=x pour obtenir la valeur numérique de GAMMA^(-1)(x) à la précision fixée par la variable d'environnement Digits.
Pour obtenir une bonne approximation de GAMMA^(-1)(x), nous employons le calcul asymptotique. Commençons par considérer un développement asymptotique de ln(GAMMA(z)) pour z au voisinage de l'infini positif.
> asympt(ln(GAMMA(z)),z,5);
![]()
Nous tronquons le développement de manière à disposer d'un majorant et d'un minorant de la fonction, du moins asymptoqtiquement.
> lb:=convert(asympt(ln(GAMMA(z)),z,3),polynom);
![]()
> ub:=convert(asympt(ln(GAMMA(z)),z,5),polynom);
![]()
Nous comparons graphiquement les fonctions ainsi définies.
> triple:=[lb,ln(GAMMA(z)),ub];
![]()
![]()
> plot(triple,z=2..10,color=[blue,red,blue],thickness=[1,3,1]);
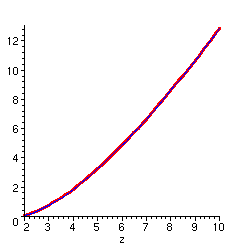
En fait d'encadrement, les approximations sont si bonnes que l'on n'arrive pas à distinguer les trois graphes. Ce phénomène s'explique par le deuxième formule de Binet sur la fonction GAMMA [WhWa27, chap. XII, sect. 12.32, pp. 250-251],
![[Maple Math]](images/ex3_32.gif) .
.
Dans cette formule, si z est un réel positif, l'arc tangente de t/z est compris entre 0 et t/z et avec l'intégrale suivante,
> 2*int(t/(exp(2*Pi*t)-1),t=0..infinity);
![]() .
.
Nous obtenons exactement l'encadrement par les deux quantités ub et lb définies plus haut.
Puisque l'approximation de ln(GAMMA(z)) par ce développement asymptotique est si bonne, nous avons envie d'inverser ce développement pour obtenir une bonne approximation de GAMMA^(-1)(x). Pour réaliser cette inversion, nous devons d'une part écrire l'équation GAMMA(z)=x sous une forme convenable, d'autre part connaître la forme du développement cherché.
Considérons d'abord la forme du développement. Jusqu'à ce jour, Maple ne sait effectuer que des développements asymptotiques suivant les puissances de la variable. C'est la raison pour laquelle nous avons appliqué un peu plus haut asympt à ln(GAMMA(z)) et non pas directement à GAMMA(z) (en fait ce cas particulier est pris en compte ; la différence est plus sensible avec la fonction W, comme on va le voir plus bas). En effet un développement de GAMMA(z) doit faire apparaître la formule de Stirling et donc un terme (z/exp(1))^z*(2*Pi/z)^(1/2) et le z^z fait que ceci ne rentre pas dans l'échelle des puissances de la variable. Encore faut-il préciser qu'il ne s'agit que de pseudo-développements asymptotiques. En vérité les puissances de la variable fournissent bien une échelle asymptotique, mais les coefficients ne sont ici pas constants et même la définition des développements asymptotiques à coefficients variables n'est pas respectée [Bourbaki76, chap. V, sect. 5, page 17]. En effet les coefficients devraient rester bornés alors qu'ici on se permet des coefficients qui sont négligeables devant toutes les puissances de la variable qui sont des infiniments grands.
Quoi qu'il en soit, le fait que les développements asymptotiques au sens de Maple ne s'effectue que selon les puissances de la variable oblige à employer une variable adéquate. Prenons un autre exemple, dont nous allons voir qu'il est assez proche de celui que nous avons à traiter. Si nous cherchons une développement asymptotique à l'infini positif de la fonction W, dite de Lambert, nous avons envie d'utiliser l'instruction suivante.
> asympt(LambertW(x),x);
![]()
Le résultat est décevant. Revenons à la
définition de la fonction W. Le
nombre z est l'image de x par cette fonction si et
seulement si on a
![]() .
Cette équation se récrit
.
Cette équation se récrit
![]() ,
ce qui par substitution donne
,
ce qui par substitution donne
![]() . On en tire d'abord que z est un O(x) puis
qu'il est équivalent à ln(x) au voisinage de
l'infini. Ensuite la dernière équation se récrit
. On en tire d'abord que z est un O(x) puis
qu'il est équivalent à ln(x) au voisinage de
l'infini. Ensuite la dernière équation se récrit
![]() et on voit que z, c'est-à-dire W(x), va avoir
un développement asymptotique suivant les puissances de
L[1]=ln(x) avec des coefficients en
L[2]=ln(ln(x)). Pour faire produire un tel
développement il faut impérativement employer
L[1] comme variable principale. On procède donc comme
suit.
et on voit que z, c'est-à-dire W(x), va avoir
un développement asymptotique suivant les puissances de
L[1]=ln(x) avec des coefficients en
L[2]=ln(ln(x)). Pour faire produire un tel
développement il faut impérativement employer
L[1] comme variable principale. On procède donc comme
suit.
> subs(L[1]=ln(x),asympt(LambertW(exp(L[1])),L[1]));
![]()
![[Maple Math]](images/ex3_40.gif)
![[Maple Math]](images/ex3_41.gif)
![]()
![]()
Pour ce qui est de l'équation, il faut qu'elle apparaisse comme
une équation de point fixe. Précisément, on veut
avoir une équation de la forme z=f(z) et qu'en
substituant un développement de z en fonction de
x dans le membre droit f(z) on obtienne un
développement plus précis. C'est exactement ce que nous
avons dans l'exemple précédent au sujet de la fonction
W. Ici nous partons de l'équation
![]() que nous pouvons récrire
que nous pouvons récrire
![]() .
.
En prenant le logarithme cela donne
![]() .
.
Le premier terme est dominant et pour ne pas avoir un produit nous prenons encore le logarithme. Nous obtenons l'équation
![]() .
.
Elle se résout en son terme dominant sous la forme
![]() .
.
Nous introduisons donc la variable
![]() et nous avons l'équation de point fixe
et nous avons l'équation de point fixe
![]() .
.
Le dernier terme du membre droit admet un développement asymtotique qui comporte des puissances de lambda et de exp(-lambda). Toutes les exponentielles sont négligeables suivant les puissances de lambda. Nous simplifions donc l'équation en évacuant les exponentielles. Cette nouvelle équation
![]()
produira le même développement asymptotique.
Par itération, nous allons obtenir une série asymptotique de la forme
![[Maple Math]](images/ex3_52.gif)
où P[k] est un polynôme. En conséquence, nous obtiendrons pour z=GAMMA^(-1)(x) un développement asymptotique de la forme
![[Maple Math]](images/ex3_53.gif)
où Q[k] est un polynôme.
Il suffit de procéder par itération pour obtenir les termes de ce développement.
> equ:=L[2]-ln(lambda)-ln(1-1/lambda);
![]()
> da:=L[2]:
to 6 do
da:=asympt(map(collect,subs(ln(L[2])=L[3],
asympt(subs(lambda=da,equ),L[2])),L[3]),L[2])
od;
![]()
![[Maple Math]](images/ex3_56.gif)
![[Maple Math]](images/ex3_57.gif)
![]()
![[Maple Math]](images/ex3_59.gif)
![[Maple Math]](images/ex3_60.gif)
![[Maple Math]](images/ex3_61.gif)
![[Maple Math]](images/ex3_62.gif)
![[Maple Math]](images/ex3_63.gif)
![[Maple Math]](images/ex3_64.gif)
![[Maple Math]](images/ex3_65.gif)
![[Maple Math]](images/ex3_66.gif)
![]()
![[Maple Math]](images/ex3_68.gif)
![[Maple Math]](images/ex3_69.gif)
![]()
En prenant l'exponentielle, nous obtenons le développement annoncé de z=GAMMA^(-1)(x).
> DA:=asympt(exp(da),L[2]);
![[Maple Math]](images/ex3_71.gif)
![[Maple Math]](images/ex3_72.gif)
![[Maple Math]](images/ex3_73.gif)
> DA:=subs(exp(L[2])=L[1],exp(-L[3])=1/L[2],DA);
![[Maple Math]](images/ex3_74.gif)
![[Maple Math]](images/ex3_75.gif)
![]()
Finalement, nous avons obtenu l'approximation suivante de la fonction inverse GAMMA^(-1).
> approx:=convert(DA,polynom);
![[Maple Math]](images/ex3_77.gif)
![[Maple Math]](images/ex3_78.gif)
On peut comparer graphiquement la fonction GAMMA^(-1) et son approximation.
> plot([[GAMMA(x),x,x=2..5],[x,subs(z=approx,L[3]=ln(L[2]),
L[2]=ln(L[1]),L[1]=ln(x),z),x=3..30]],color=[red,blue]);
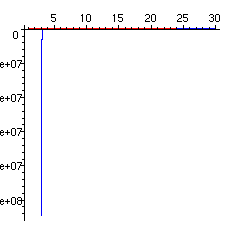
> plot([[GAMMA(x),x,x=2..5],[x,subs(z=approx,L[3]=ln(L[2]),
L[2]=ln(L[1]),L[1]=ln(x),z),x=5..30]],color=[red,blue]);
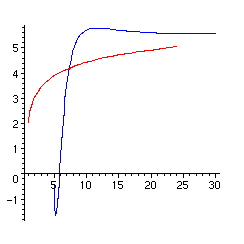
> plot([[GAMMA(x),x,x=5..6.5],[x,subs(z=approx,L[3]=ln(L[2]),
L[2]=ln(L[1]),L[1]=ln(x),z),x=20..300]],color=[red,blue]);
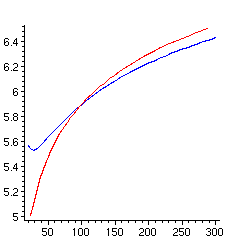
Pour le premier dessin, il y a divergence à cause du logarithme itéré trois fois L[3]. Par ailleurs l'approximation n'est pas de bonne qualité, alors que nous étions partis d'un développement qui collait à la fonction. Cela est dû au fait que le développement de l'inverse se fait suivant les puissances de L[2] et ne prend en compte que les premiers termes du développement de ln(GAMMA(z)). On aimerait tenir compte d'autres termes et avoir un développement suivant les puissances de L[1], mais la théorie classique ne le permet pas. Nous reviendrons un peu plus loin sur ce point avec les multiséries.
Maintenant que nous disposons d'une approximation, nous appliquons la méthode de Newton à l'équation GAMMA(z)=x en partant de cette approximation. Appliquer la méthode de Newton revient à itérer la fonction
![]() .
.
Il faut toutefois modérer un peu notre ardeur. L'approximation obtenue s'exprime en fonction de L[1]=ln(x), L[2]=ln(ln(x)), L[3]=ln(ln(ln(x))). Encore faut-il que ces quantités existent. Ceci revient à dire que x est plus grand que exp(1). De plus il est prudent de se limiter aux nombres positifs, y compris pour L[3]=ln(ln(ln(x))). Pour rester simples, nous distinguons deux cas suivant la place de x par rapport à 20.
Dans le cas où x est entre 1 et 20 nous partons du point z=4.5. Précisons que nous avons testé cette séquence d'instructions avec différentes valeurs pour le point de départ et le choix z=4.5 a semblé satisfaisant. Il est d'ailleurs amusant de voir ce que produit l'itération.
> f:= z-(GAMMA(z)-x)/(Psi(z)*GAMMA(z));
![]()
> plot([[GAMMA(x),x,x=2..5],[x,subs(z=4.5,f),x=1..20]],
color=[red,blue]);
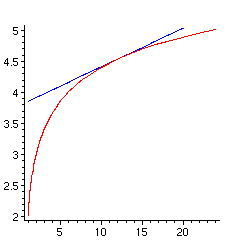
> ff:=subs(z=f,f);
![[Maple Math]](images/ex3_85.gif)
> plot([[GAMMA(x),x,x=2..5],[x,subs(z=4.5,ff),x=1..20]],
color=[red,blue]);
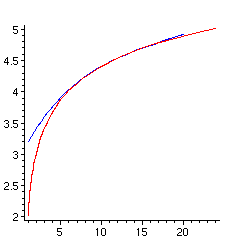
> fff:=subs(z=f,ff):
> plot([[GAMMA(x),x,x=2..5],[x,subs(z=4.5,fff),x=1..20]],
color=[red,blue]);
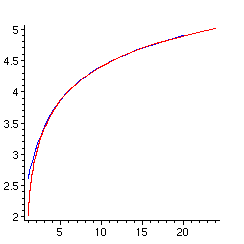
Au bout de trois applications de la fonction, on a une bonne approximation de l'inverse GAMMA^(-1).
Au dessus de 20, nous prenons comme valeur initiale l'approximation que nous avons trouvée pour GAMMA^(-1)(x). Nous pourrions procéder à la même expérience que ci-dessus en traçant quelques dessins.
La procédure evalf/invGAMMA comporte trois phases. On commence (#1) par donner le point de départ de l'itération de Newton. Ensuite (#2) on applique l'itération quelques coups pour obtenir une bonne approximation. Jusqu'ici on a travaillé avec un nombre faible de chiffres pour que les calculs ne soient pas trop coûteux. Enfin on calcule le résultat demandé en doublant la précision à chaque tour de boucle (on sait que la méthode de Newton est une méthode d'ordre 2), jusqu'à arriver à la précision souhaitée.
> `evalf/invGAMMA`:=proc(x::algebraic)
local xx,oldDigits,L,oldz,newz,GAMMAoldz;
xx:=evalf(x);
if not type(xx,float) then RETURN(`invGAMMA`(x)) fi;
oldDigits:=Digits;
Digits:=5; #1
if xx>=20 then
L[1]:=ln(xx):
L[2]:=ln(L[1]);
L[3]:=ln(L[2]);
newz:=L[1]*(1/L[2]+(L[3]+1)/(L[2]^2)
+(L[3]^2+L[3])/(L[2]^3)
+(L[3]^3+1/2*L[3]^2-L[3]-1/2)/(L[2]^4)
+(L[3]^4-1/3*L[3]^3-5/2*L[3]^2-L[3]+1/6)/(L[2]^5)
+(11/6*L[3]-23/6*L[3]^3-17/12*L[3]^4+L[3]^5+5/12)
/(L[2]^6));
elif xx>=1. then
newz:=4.5;
else
ERROR("evalf/invGAMMA expects its argument to be
not smaller than 1, but received ",x)
fi;
while evalf(newz,Digits-1)<>evalf(oldz,Digits-1) do #2
oldz:=newz;
newz:=oldz-(GAMMA(oldz)-xx)/Psi(oldz)/GAMMA(oldz);
od;
Digits:=3; #3
while oldDigits>Digits do
Digits:=min(2*Digits,oldDigits+5);
oldz:=newz;
GAMMAoldz:=GAMMA(oldz);
newz:=oldz-(GAMMAoldz-xx)/Psi(oldz)/GAMMAoldz;
od;
evalf(newz,oldDigits)
end:
Testons un peu la procédure.
> Digits:=50:
> xxx:=19.5;
![]()
> start:=time():
zzz:=`evalf/invGAMMA`(xxx);
time()-start;
![]()
![]()
> GAMMA(zzz);
![]()
> xxx:=20.5;
![]()
> start:=time():
zzz:=`evalf/invGAMMA`(xxx);
time()-start;
![]()
![]()
> GAMMA(zzz);
![]()
Maintenant que nous disposons d'une procédure de calcul numérique relativement efficace, il devient réaliste de tracer le graphe de GAMMA^(-1). Nous le comparons avec le graphe obtenue à partir de celui de GAMMA par symétrie par rapport à la diagonale.
> Digits:=10:
> plot([[GAMMA(z),z,z=2..4],[x,invGAMMA(x),x=1..6]],
color=[red,blue]);
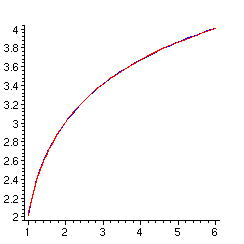
L'accord est, à l'oeil, excellent.
Multiséries. Nous avons vu que la théorie classique des développements asymptotiques n'est pas assez puissante. Alors que nous disposions d'un bon développement pour GAMMA, cette théorie ne fournit qu'un développement peu satisfaisant pour GAMMA^(-1). En effet il ne s'appuie que sur les premiers termes du développement de GAMMA. Le développement obtenu suivant les puissances de L[2]=ln(ln(x)) ne permet pas d'atteindre ce qui est derrière le premier terme en L[1]=ln(x). Autrement dit on aimerait aller au delà de l'infini.
La réponse à ce souhait est la théorie des multiséries. Elle est présentée dans [RiSaShVH96] (postscript|html). Essentiellement une multisérie est un développement suivant les puissances (non nécessairement entières) d'une fonction f à coefficients des multiséries qui s'expriment à l'aide de fonctions à variations plus lentes. Une échelle asymptotique, dans cette théorie, est constituée d'un ensemble fini de fonctions ; pour un développement du type précédent, la première fonction de l'échelle est f. La notion d'échelle n'est pas la notion classique de la théorie des développements asymptotiques.
Pour ce qui concerne les fonctions inverses, notre sujet dans cet exercice, la théorie en a été faite dans [SaSh97] (postscript). Bruno Salvy a mis au point un package Maple pour calculer les multiséries de fonctions inverses. Ce package n'est pas public et vous ne pouvez donc pas exécuter ce qui suit. Nous le présentons pour mettre en valeur ce qu'apporte cette nouvelle théorie.
Nous commençons par calculer un développement asymptotique de GAMMA, puis nous tronquons le développement en évacuant le grand O.
> asympt(GAMMA(y),y);
![]()
![]()
![]()
> eval(subs(O=0,%));
![]()
![]()
Nous en appelons à la procédure Invert qui va déterminer les donnéees nécessaires au calcul des développements asymptotiques de l'inverse et en particulier l'échelle utilisée (insistons sur le fait que la notion d'échelle n'est pas la notion classique).
> r:=Invert(%,y,'S');
![[Maple Math]](images/ex3_salvy_6.gif)
![[Maple Math]](images/ex3_salvy_7.gif)
![[Maple Math]](images/ex3_salvy_8.gif)
![[Maple Math]](images/ex3_salvy_9.gif)
![]()
Ensuite on peut calculer les développements que l'on désire pour GAMMA^(-1). La précision des développements est déterminée par les paramètres numéro 2 et 3. Les paramètres numéro 4 et 5 ont à peu près le même sens que les deux derniers paramètres dans series ou asympt. Pour de faibles valeurs on voit seulement le L[1]=ln(x) qui est le comportement essentiel de l'inverse.
> multiseriesinverse([r],S,0,0,x,3);
![]()
> multiseriesinverse([r],S,0,1,x,3);
![]()
Si l'on augmente ces paramètres numéro 2 et 3, le développement classique, que nous avons calculé plus haut, apparaît.
> multiseriesinverse([r],S,0,2,x,5);
![[Maple Math]](images/ex3_salvy_13.gif)
![[Maple Math]](images/ex3_salvy_14.gif)
![[Maple Math]](images/ex3_salvy_15.gif)
![[Maple Math]](images/ex3_salvy_16.gif)
Si l'on augmente encore les paramètres, on va au delà du développement classique avec un terme constant 1/2, un terme en 1/L[2], un grand O de 1/L[2] et ces termes constituent le coefficient de L[1]^0, puis le terme en L[1]^(-1). Bref on a un développement suivant les puissances de L[1] à coefficients des développements suivant les puissances de L[2].
> multiseriesinverse([r],S,1,2,x,3);
![[Maple Math]](images/ex3_salvy_17.gif)
![[Maple Math]](images/ex3_salvy_18.gif)
> multiseriesinverse([r],S,0,3,x,5);
![[Maple Math]](images/ex3_salvy_27.gif)
![[Maple Math]](images/ex3_salvy_28.gif)
![[Maple Math]](images/ex3_salvy_29.gif)
![[Maple Math]](images/ex3_salvy_30.gif)
![[Maple Math]](images/ex3_salvy_31.gif)
![[Maple Math]](images/ex3_salvy_32.gif)
![[Maple Math]](images/ex3_salvy_33.gif)
![[Maple Math]](images/ex3_salvy_34.gif)
![]()
![[Maple Math]](images/ex3_salvy_36.gif)
![[Maple Math]](images/ex3_salvy_37.gif)
On pourrait arguer que ce qui suit le développement classique est une illusion puisque le L[1]*O(1/L[2]^3) masque ces termes. Mais ce serait douter de la science car nous pouvons aussi disposer d'une expression exacte.
> multiseriesinverse([r],S,2,3,x,3);
![]()
![[Maple Math]](images/ex3_salvy_22.gif)
![[Maple Math]](images/ex3_salvy_23.gif)
![[Maple Math]](images/ex3_salvy_24.gif)
![]()
![[Maple Math]](images/ex3_salvy_26.gif)
On voit appraître dans le RootOf l'équation qui nous a permis d'obtenir le développement classique par itération.
La théorie garantit que le développement de type multisérie se fait suivant les puissances des fonctions qui apparaissent dans la liste suivante et que celles-ci suffisent.
> S[list];
![]()
Ces fonctions constituent l'échelle évoquée plus haut.