Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Nous définissons le polynôme par son expression.

> f:=x^5+3*x^4+x^2+8*x+3;

Pour chercher graphiquement les racines réelles du polynôme, nous commençons par déterminer un intervalle qui les contient. Pour cela nous employons l'inégalité valable pour tout réel x. Si désigne la valeur absolue d'une racine x, alors ce nombre satisfait ou rho>=1 et et donc . Ceci fournit une borne sur la taille des racines. Cette borne est d'ailleurs aussi valable pour les racines complexes. Muni de cette borne, nous pouvions étudier graphiquement la question.

> plot(f,x=-15..15);

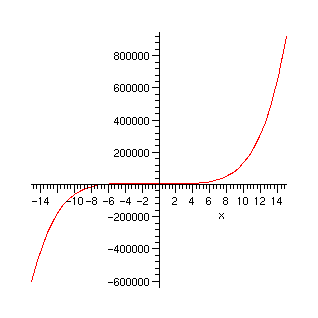
> plot(f,x=-8..5);

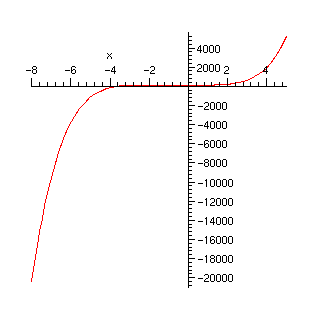
> plot(f,x=-4..2);

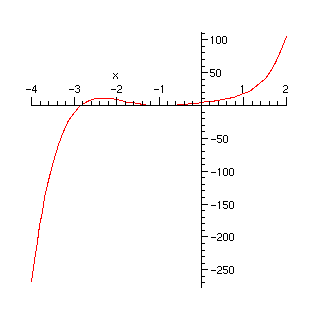
Nous pourrions continuer à procéder par raffinements successifs. Cela revient grosso modo à l'application de la méthode de dichotomie. La procédure fsolve nous permet de calculer numériquement les racines réelles ou complexes.

> fsolve(f,x=-3..0);

> fsolve(f,x,complex);

Les racines réelles sont négatives puisque les coefficients du polynôme sont positifs.

Retour en page principale