Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Maple fournit le développement d'arc sinus en 0 à tout ordre.

> series(arcsin(x),x,10);

Mais ceci ne nous avance en rien. Heureusement nous connaissons par coeur le développement en série entière d'arc sinus en 0,

,  .

Mais ce n'est pas ce dont nous avons besoin ; une formule de Taylor avec un reste explicite est bien plus adaptée. Plutôt, une majoration explicite du reste nous est utile. Suivant [Bourbaki76, Chap. III, pp. 22--23], nous pouvons écrire

,

avec

,  .

Cette inégalité permet de calculer le nombre de chiffres décimaux utile pour mener le calcul.

Nous commençons en définissant le terme général de la somme.

> xx:=1/2:

> term:=6*product(2*k-1,k=1..n)/

                      product(2*k,k=1..n)*xx^(2*n+1)/(2*n+1);

Ensuite, au lieu d'appliquer la théorie correcte que nous avons rappelée ci-dessus, nous nous comportons en praticien béat. Nous nous contentons d'évaluer la taille du dernier terme de la somme pour décider du nombre de chiffres à employer. Ceci est contraire au bon sens et revient à faire l'hypothèse que le terme d'indice N et le reste d'indice N sont grosso modo du même ordre de grandeur. Mais l'analyse n'est pas mauvaise fille et même plutôt généreuse. Ici le dernier terme est en alors que le reste est en , ce qui n'est pas trop différent, et ceci conforte le praticien béat dans ses mauvaises pratiques. Il suffit de penser à la série des , dont le terme d'indice N est alors que le reste d'indice N est en , pour comprendre que cette façon de faire peut conduire à des résultats illusoires. On pourrait rétorquer que dans cet exemple, on augmente inutilement la précision des calculs mais que cela ne nuit pas au résultat. Seule l'efficacité du calcul est compromise. L'exemple de la série des , dont le terme d'indice N est alors que le reste d'indice N est en suffit à montrer que cette objection est sans valeur.

Nous évaluons donc le nombre de chiffres utile de la manière illusoire que nous venons de décrire.

> asympt(term,n,3);

> combine(%,exp,symbolic);

> combine(%,power,symbolic);

> d:=solve(1/4*(1/n)^(3/2)/(sqrt(Pi))*2^(-2*n)=10^(-digits),

                                          digits);

Nous laissons le lecteur corriger cette phase de calcul mal fondée. Ensuite nous calculons pour chaque entier de 1 à 10 la différence entre et ce que fournit la somme partielle.

> for nn to 10 do 

    Digits:=floor(1.1*subs(n=nn,d)+5);

    evalf(Pi-add(evalf(subs(n=k,term)),k=0..nn))

  od;

Tout a l'air normal. Nous en venons donc à la question posée. Nous rangeons dans la table correct le nombre de décimales correctes fournies par le calcul. Ce nombre s'obtient en employant le logarithme de base 10. La valeur absolue n'est pas utile dans ce cas particulier parce qu'ici la différence que nous obtenons est positive ; nous ne la mettons que dans un souci de généralité.

> for nn to 100 do 

    Digits:=floor(1.1*subs(n=nn,d)+5);

    correct[nn]:=floor(-log[10](abs(evalf(

                   Pi-add(evalf(subs(n=k,term)),k=0..nn)))))

  od:

> Digits;

Le calcul précédent est bien peu efficace, puisque nous recalculons à chaque étape la somme partielle précédente. Il est plus simple de fixer d'emblée Digits à la précision maximale désirée. Nous reprenons donc le calcul depuis son début en ouvrant une nouvelle session (sinon la comparaison des deux modes de calcul est illusoire car le logiciel garde en mémoire les calculs déjà effectués). Insistons cependant sur le fait que dans d'autres cas le calcul précédent pourrait être le plus performant. Il suffirait pour cela que Digits augmente très fortement d'un rang au suivant.

> xx:=1/2:

> term:=6*product(2*k-1,k=1..n)/

                product(2*k,k=1..n)*xx^(2*n+1)/(2*n+1):

> Digits:=75:

> S:=subs(n=0,term):

  for nn to 100 do 

    S:=evalf(S+subs(n=nn,term));

    delta:=abs(evalf(Pi-S));    

    correct[nn]:=floor(-log[10](delta))

  od:

> plot([seq([k,correct[k]],k=0..100)],

                 style=point,symbol=circle,scaling=constrained);

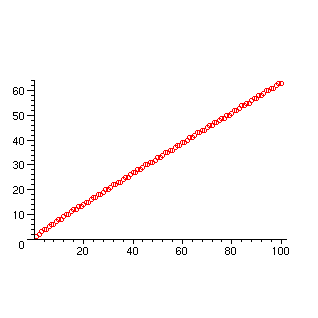
On voit que grosso modo les points s'alignent sur une droite. Le nombre de décimales correctes gagnées à chaque cran est à peu près constant (environ six décimales). On traduit ceci en disant que la méthode de calcul est d'ordre 1.

On trouvera d'autres modes de calcul de dans [BaBoBoPl97] (article de vulgarisation facile à lire et qui permet de plaisantes expériences) ou [BoBo87] (livre plus technique).

Retour en page principale