Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Nous définissons les deux expressions de fonction, puis nous traçons les graphes.

> f1:=y^2-x^2:

  f2:=2/3+cos(x)-cos(y):

> r:=-1..1:

> p1:=plot3d(f1,x=r,y=r,color=blue):

> p2:=plot3d(f2,x=r,y=r,color=red):

> plots[display]({p1,p2});

En choisissant bien l'orientation, nous nous convaincons que les deux graphes sont disjoints et que la fonction est plus grande que la fonction .

> plots[display]({p1,p2},orientation=[20,90]);

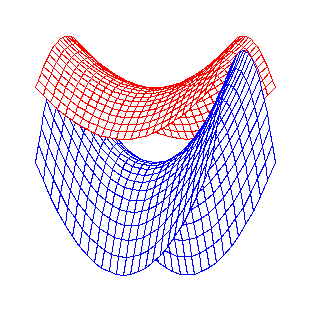
La question se ramène à l'étude de fonctions d'une variable. Les calculs et dessins suivants le montrent aisément.

> g1:=1-x^2:

  g2:=cos(x):

> q1:=plot(g1,x=r,color=blue):

> q2:=plot(g2,x=r,color=red):

> plots[display]({q1,q2});

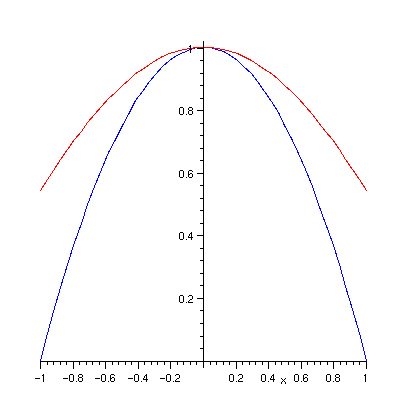
> h1:=y^2-1:

  h2:=2/3-cos(y):

> r1:=plot(h1,y=r,color=blue):

> r2:=plot(h2,y=r,color=red):

> plots[display]({r1,r2});

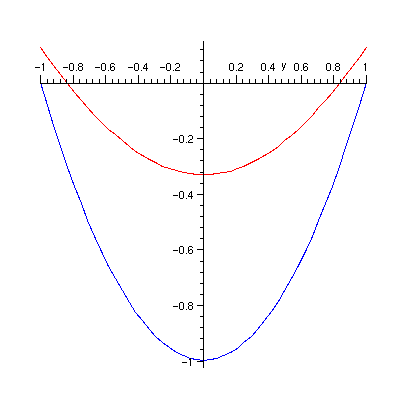
Il suffit de considérer les dérivées premières et secondes de et pour conclure.

> diff(g2-g1,x);

> diff(h2-h1,y);

Retour en page principale