Gomez, Salvy, Zimmermann. Chapitre IV, section 1.5, exercice 2, page 107.

Calcul formel : Mode d'emploi - Exemples en Maple

Claude Gomez, Bruno Salvy, Paul Zimmermann

Masson, 1995

Chapitre IV, section 1.5, exercice 2, page 107.

Philippe.Dumas@inria.fr
http://algo.inria.fr/dumas/Maple/

Page du Projet Algorithmes | Page de Philippe Dumas | Page Maple de Philippe Dumas

Retour en page principale
Table des matières
Index

Maple V.4 worksheet
Maple V.5 worksheet

Courbes elliptiques | Calcul automatique des opérations
L'exercice lui-même | Tests sur des courbes elliptiques

Courbes elliptiques. La première question qui vient à l'esprit en lisant l'énoncé est : y a-t-il des cas où la division ne coûte pas plus cher que la multiplication ? Pour répondre à cette question et replacer l'exercice dans son contexte, nous commençons par une digression.

Une cubique non singulière peut être munie d'une loi de groupe. Considérons une cubique de la forme

> f:=x*(x^2+y^2)-a*(x^2+y^2)-b*x-c*y;

par exemple celle que voici.

> f1:=subs(a=1,b=1,c=-1,f);

Le package algcurves (nous employons la version V.5) nous permet de vérifier que cette cubique est de genre 1.

> algcurves[genus](f1,x,y,`irr check`);

De plus il nous fournit la forme de Weierstrass de cette courbe. C'est la première opérande de la liste fournie en réponse ci-dessous.

> w1:=algcurves[Weierstrassform](f1,x,y,u,v);

[Maple Math]

Moyennant la transformation birationnelle fournie par les termes d'indices 2 et 3 de cette liste l'équation est ramenée à la forme de Weierstrass. Il faut comprendre que la transformation s'écrit u=(y-1)/(x-1), v=x*(x-2+y)/(1-x)^2. Les deux composantes suivantes donnent la transformation réciproque.

La forme de Weierstrass permet de tracer la cubique dans le repère en u, v et par simple substitution dans le repère d'origine.

> V:=[solve(w1[1],{v})];

> for i to 2 do arc[i]:=subs(V[i],[w1[4],w1[5]]) od;

[Maple Math]

À cause de la racine carré, il faut sélectionner les intervalles corrects limités par les racines réelles du polynôme du troisième degré qui figure sous le radical. Nous procédons de façon relativement générique.

> p:=select(has,w1[1],u):

> lp:=-coeff(p,u,3):

> proot:=[fsolve(p,u)]:

> if nops(proot)=1 then

    nb:=1;

    if lp>0 then r[1]:=proot[1]..infinity

    else r[1]:=-infinity..proot[1]

    fi

  else

    nb:=2;

    proot:=sort(proot);

    if lp>0 then 

      r[1]:=proot[1]..proot[2];

      r[2]:=proot[3]..infinity

    else 

      r[1]:=-infinity..proot[1];

      r[2]:=proot[2]..proot[3]

    fi

  fi:

> for i to nb do

    picture[i,1]:=plot([arc[1][1],arc[1][2],u=r[i]]);

    picture[i,2]:=plot([arc[2][1],arc[2][2],u=r[i]])

  od:

Nous obtenons ainsi un dessin de la cubique.

> plots[display]({seq(op([picture[i,1],picture[i,2]]),i=1..nb)},

                                             view=[-1..2,-6..6]);

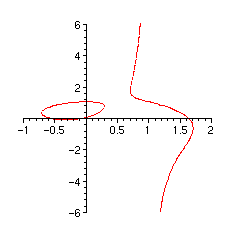
Nous le gardons au chaud, car il va resservir.

> picture[curve]:=

  plots[display]({seq(op([picture[i,1],picture[i,2]]),

                               i=1..nb)},color=red,thickness=3):

Venons en à la loi de groupe. Pour l'illustrer nous choisissons quelques points sur la cubique, en tenant compte des intervalles que nous avons déterminés. Le point N va être le neutre de cette loi de groupe. Il faut préciser que la loi est notée additivement, car elle est commutative. Nous allons montrer comment additionner les deux points P et Q.

> eval(r);

> N:=subs(u=1/2,arc[2]);

> P:=subs(u=-2,arc[1]);

> Q:=subs(u=-3,arc[2]);

Nous définissons la droite PQ sous forme paramétrique. Au passage nous la dessinons. Ensuite nous calculons les points d'intersection de la droite PQ et de la cubique. Évidemment les deux points P et Q sont dans l'intersection. L'équation en t, obtenue en reportant le paramétrage de la droite dans la cubique, est du troisième degré et possède une troisième solution. C'est celle que nous cherchons et qui nous fournit le point R.

> PQpt:=[(1-t)*P[1]+t*Q[1],(1-t)*P[2]+t*Q[2]];

> picture[PQ]:=plot([PQpt[1],PQpt[2],t=-3..3],view=[-1..2,-6..6],

                                                  color=blue):

> tt:=[solve(collect(subs(x=PQpt[1],y=PQpt[2],f1),t,radnormal),

                                                            {t})];

> tt:=op(remove(has,tt,{{t=0},{t=1}}));

> R:=map(radnormal,subs(tt,PQpt));

Par définition de la loi, la somme P+Q+R est nulle (c'est-à-dire vaut le point N). Nous avons donc R=-(P+Q). Il suffit, pour obtenir P+Q, de calculer le point S tel que R+S+N soit nul, c'est-à-dire le troisième point de la droite RN qui est sur la cubique. Allons y.

> RNpt:=[(1-t)*R[1]+t*N[1],(1-t)*R[2]+t*N[2]];

> picture[RN]:=plot([RNpt[1],RNpt[2],t=-3..3],view=[-1..2,-6..6],

                                                       color=blue):

> tt:=[solve(collect(subs(x=RNpt[1],y=RNpt[2],f1),t,radnormal),

                                                          {t})];

> tt:=op(remove(has,tt,{{t=0},{t=1}}));

> S:=map(radnormal,subs(tt,RNpt));

Nous avons ainsi obtenu le point S=P+Q. Finissons d'illustrer la situation.

> picture[points]:=plot({P,Q,R,N,S},style=point,symbol=circle,

                                                  color=black):

> picture[text]:=plots[textplot](

  [[P[1]+.1,P[2]+.1," P"],

   [Q[1]+.2,Q[2]," Q"],

   [R[1],R[2]-.5," R"],

   [N[1]+.1,N[2]-.2," N"],

   [S[1],S[2]-.5," S"]]):

> plots[display]({seq(picture[i],i={curve,PQ,RN,points,text})},

                              view=[-1..2,-6..6],axes=none);

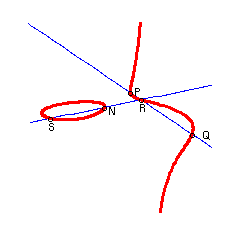
Revenons sur la définition pour la mettre au net. Nous partons d'un polynôme du troisième degré f(x,y) en deux indéterminées x et y. Ce polynôme est à coefficients dans un corps K. La cubique associée est l'ensemble algébrique défini par le polynôme dans le plan projectif P_2(K). Autrement dit la cubique a pour équation homogène F(X,Y,T)=0 avec F(X,Y,T)=T^3*f(X/T,Y/T). Dans l'exemple précédent le polynôme est à coefficients entiers donc on peut considérer que le corps de base est le corps Q des rationnels. Cependant les points que nous avons choisis ont leur coordonnées dans le corps Q(sqrt(2),sqrt(3)) et c'est donc ce corps que nous utilisons. Évidemment on pourrait bien considérer que les calculs se font dans le corps des réels ou le corps des complexes, mais il y a au moins deux raisons de ne pas le faire. D'abord les propriétés de la cubique dépendent du corps utilisé. Ensuite les eléments du corps Q(sqrt(2),sqrt(3)) sont représentables de manière fini, ce qui n'est pas le cas des réels ou des complexes, et on peut donc calculer dans ce corps.

Il faudrait justifier que la loi obtenue sur la cubique est une loi de groupe. Notons d'abord que la définition est correcte. Précisément si P et Q sont deux points de la cubique, les coordonnées de ces deux points et les coefficients de l'équation de la cubique sont dans le corps K. Quand on écrit une équation paramétrique de la droite PQ, comme nous l'avons fait, et qu'on la reporte dans l'équation homogène de la cubique on n'emploie que des opérations rationnelles et l'équation du troisième degré obtenue est à coefficients dans K. Les deux racines qui correspondent à P et Q sont dans K et donc aussi la troisième puisque la somme des racines est donnée par les coefficients de l'équation. Finalement le point R=-(P+Q) est à coordonnées dans K. En reprenant le même raisonnement avec R et le point neutre N, on voit que la somme S=P+Q est à coordonnées dans K.

Le reste se prouve sans trop de mal. Le seul point délicat est l'associativité ; elle découle du théorème des neufs points qui apparaît dans l'exercice 6 de la page 167. On peut montrer que si l'on change de point neutre sur la cubique, les deux groupes obtenus sont isomorphes.

Calcul automatique des opérations. Maintenant nous mettons au point une procédure EC (pour Elliptic Curve) qui va permettre d'associer à une cubique les opérations sur cette cubique. Vue la longueur du code, il est préférable d'employer un éditeur de texte. Nous écrivons donc le code dans un fichier EC_V5.mpl. Nous écrivons aussi une version EC_V3.mpl valable en Maple V.3 (et acceptable en Maple V.4).

La procédure EC prend en entrée un polynôme de degré 3, qui fournit l'équation ou l'équation homogène d'une cubique ; la liste des indéterminées utilisées dans le polynôme précédent ; le couple ou le triplet qui définit le neutre de la courbe elliptique. Ces données ne sont pas vérifiées. Une quatrième argument optionnel est une procédure qui fournit une forme normale pour les éléments du corps K. Par forme normale nous entendons que le zéro a pour seule écriture 0. Enfin un cinquième argument optionnel est une procédure de réduction dont on espère qu'elle modérera la croissance des expressions.

La valeur par défaut de la procédure de normalisation est l'identité. Même si le quatrième argument est optionnel, il est nécessaire que le procédure fournisse une forme normale pour que les résultats soient garantis.

Pour la cubique étudiée précédemment, on emploie donc la procédure comme suit. Puisque le corps de base est Q(sqrt(2),sqrt(3), il est naturel d'utiliser la procédure radnormal comme procédure de réduction. Pour la procédure de réduction, simplify/radical ferait tout aussi bien l'affaire que radnormal.

> read "EC.mpl";

> ec1:=EC(f1,[x,y],N,radnormal,radnormal):

La procédure EC renvoie une table dont les indices sont les noms globaux Equ, Nullpt, Isequal, Add, Double, Opposite, Subt, Ext1, Ext2.

La valeur d'indice Equ est simplement le polynôme ec donné en entrée ;
la valeur d'indice Nullpt est le triplet des coordonnées homogènes du point neutre, fourni en entrée ;
la valeur d'indice Isequal est une procédure à valeurs booléennes qui prend en entrée deux triplets d'éléments du corps K (ceci n'est pas vérifié). Elle renvoie vrai si et seulement les deux triplets définissent le même point de l'espace projectif (mais on ne teste pas le cas où l'un des triplets serait le triplet nul) ;
la valeur d'indice Add est une procédure de calcul qui réalise l'addition sur la cubique. Elle prend en entrée deux triplets d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés ;
la valeur d'indice Double réalise la multiplication par 2. Elle prend en entrée un triplet d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés ;
la valeur d'indice Opposite réalise le moins unaire. Cette procédure prend en entrée un triplet d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés ;
la valeur d'indice Subt réalise la soustraction sur la cubique. Elle prend en entrée deux triplets d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés ;
la valeur d'indice Ext1 réalise la version additive de l'exponentiation binaire. Cette procédure prend en entrée un entier et un triplet d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés ;
la valeur d'indice Ext2 réalise la version additive de l'exponentiation binaire améliorée, qui est demandée dans l'énoncé de l'exercice. Cette procédure prend en entrée un entier et un triplet d'éléments de K et renvoie un triplet d'éléments de K. Les arguments ne sont pas vérifiés.

Testons la procédure en reprenant le calcul que nous avons effectué à la main. Les procédures renvoyées par EC emploient les coordonnées homogènes et nous commençons donc par passer dans ces coordonnées. Ensuite nous calculons la somme de P et Q, qui sont maintenant pt2 et pt3.

> Lpt:=[N,P,Q,R,S]:

> for i to nops(Lpt) do

    pt.i:=[Lpt[i][1],Lpt[i][2],1]

  od;

> pt6:=ec1[Add](pt2,pt3);

Le résultat est rangé dans pt6, alors que la somme S calculée précédemment a été mise dans pt5. Nous testons l'égalité des deux résultats.

> ec1[Isequal](pt5,pt6);

Tout paraît normal.

L'exercice lui-même. Revenons à l'exercice proposé. Le code qui est utilisé dans EC pour écrire la procédure ext2 n'est qu'une reprise de l'article de F. Morain et J. Olivos, Speeding up the computations on an elliptic curve using addition-subtraction chains (référence bibtex). Vous trouverez cet article en format Postscript dans les publications de François Morain (c'est le chapitre 4 de sa thèse Courbes elliptiques et tests de primalité ; voir Articles, Other publications dans sa page) ou ici en format Gif.

L'exponentiation binaire usuelle, dans sa version multiplicative, consiste à calculer d'abord l'écriture binaire de l'exposant n, puis à l'utiliser de la manière suivante : pour calculer x^n, on introduit deux variables y et z ; dans y on range successivement x, x^2, x^4, ... obtenus par des elévations au carré successives et en passant on accumule dans z les produits z*y quand le bit correspondant de n vaut 1. L'idée de l'article est de remplacer une chaîne de 1 dont la longueur est a, disons 1^a, par la chaîne 10^(a-1)(-1), où le dernier -1 correspond à une division. Ceci fait considérer l'automate de la figure 1 (nous faisons référence à l'article). Une seconde amélioration conduit à l'automate de la figure 2 et c'est cet automate que nous avons utilisé pour écrire le code de ext2.

Bien sûr, l'exercice ne demandait pas une digression aussi longue, ni la connaissance de l'article de F. Morain et J. Olivos. Cependant, d'une manière ou d'une autre, l'emploi d'un automate est la voie naturelle pour représenter la situation. La solution obtenue doit donc avoir l'allure suivante, même si plusieurs automates peuvent faire l'affaire.

> expodiv:=proc(n::integer,x)

    local L,y,z,i,state;

    if n=0 then 1

    elif n<0 then expodiv(-n,1/x)

    else

      L:=convert(n,base,2);

      y:=1; 

      z:=x;

      state:=0;

      for i to nops(L) do

        if L[i]=0 then 

	  if state=0 then

	    z:=z^2

	  elif state=1 then

	    y:=y*z;

	    z:=(z^2)^2; 

	    state:=0 

          else

	    state:=1

	  fi;

        else

	  if state=0 then 

	    state:=1

          else 

	    if state=1 then

	      y:=y/z;

	      z:=z^2;

	      state:=11

	    fi;

	    z:=z^2

	  fi

        fi;

      od;

      y*z

    fi

  end:

> expodiv(31,x);

Le calcul est correct mais apporte peu à la compréhension. La version suivante est plus parlante.

> expodiv:=proc(n::integer,x)

    local L,y,z,i,state;

    if n=0 then 1

    elif n<0 then expodiv(-n,1/x)

    else

      L:=convert(n,base,2);

      y:=1; 

      z:=x;

      state:=0;

      for i to nops(L) do

        if L[i]=0 then 

	  if state=0 then

	    z:=``(z)^2

	  elif state=1 then

	    y:=``(y)*``(z);

	    z:=``(``(z)^2)^2; 

	    state:=0 

          else

	    state:=1

	  fi;

        else

	  if state=0 then 

	    state:=1

          else 

	    if state=1 then

	      y:=``(y)/``(z);

	      z:=``(z)^2;

	      state:=11

	    fi;

	    z:=``(z)^2

	  fi

        fi;

      od;

      ``(y)*``(z)

    fi

  end:

> expodiv(31,x);

[Maple Math]

On voit que l'on est proche de l'exemple fourni dans l'énoncé.

Tests sur des courbes elliptiques. Cette variante de l'exponentiation binaire repose sur le fait que la multiplication et la division, dans l'exemple que nous traitons l'addition et la soustraction, ont le même coût. En effet notons P*Q le troisième point de la droite PQ qui est sur la cubique. Pour évaluer P+Q, on calcule d'abord R=P*Q, puis R*N. Pour obtenir P-Q, on commence par déterminer -P=P*N, puis on calcule (-P)*Q=P-Q. On voit bien que les deux opérations ont le même coût et cette symétrie se traduit dans le code des deux procédures locales elliptic_add et subt.

  elliptic_add:=
  subs(_isequal=isequal,_thirdpoint1=thirdpoint1,
       _thirdpoint2=thirdpoint2,_nullpt=nullpt,
       _reductionproc=reductionproc,
  proc(pt1,pt2)
    local pt;
    if _isequal(pt1,pt2) then                 # test 1
      pt:=_thirdpoint2(pt1)                   # call thirdpoint2
    else
      pt:=_thirdpoint1(pt1,pt2)               # call thirdpoint1
    fi;
    if _isequal(pt,_nullpt) then              # test 2
      _nullpt
    else
      _reductionproc(_thirdpoint1(pt,_nullpt))# call thirdpoint1
    fi                                        # call reductionproc
  end);

  subt:=
  subs(_isequal=isequal,_thirdpoint1=thirdpoint1,
       _thirdpoint2=thirdpoint2,_nullpt=nullpt,
       _reductionproc=reductionproc,
  proc(pt1,pt2)
    local pt;
    if _isequal(pt1,_nullpt) then             # test 2
      pt:=_nullpt
    else
      pt:=_thirdpoint1(pt1,_nullpt)           # call thirdpoint1
    fi;
    if _isequal(pt,pt2) then                  # test 1
      _reductionproc(_thirdpoint2(pt))        # call thirdpoint2
    else                                      # call reductionproc
      _reductionproc(_thirdpoint1(pt,pt2))    # call thirdpoint1
    fi
  end);

Nous aimerions nous convaincre que cette symétrie se traduit dans la réalité par des coûts similaires. Pour éviter des temps de calcul prohibitifs, nous allons calculer avec des nombres entiers et pour cela nous utilisons la courbe elliptique favorite de Richard K. Guy [Guy95].

> f2:=y^2-(x^3-4*x+4);

Puisque nous n'employons que des entiers (on remarquera que dans EC nous n'effectuons aucune division) la normalisation est automatique. Pour éviter une croissance excessive des entiers, nous réduisons les triplets en les simplifiant par leur pgcd.

> redproc:=proc(pt) 

    local g,i,pt1; 

    g:=igcd(op(pt)); 

    if g=0 then ERROR() 

    else pt1:=[seq(pt[i]/g,i=1..3)] 

    fi;

    if pt1[3]<0 then [seq(-pt1[i],i=1..3)] else pt1 fi;

  end:

Nous définissons les opérations sur la courbe et nous choisissons un point de la courbe. Nous allons réaliser cent additions et cent soustractions de ce point. Pour comparer valablement les résultats, nous employons exprofile. Le fichier créé par cette procédure peut être assez gros.

> ec2:=EC(f2,[x,y],[0,1,0],x->x,redproc):

> pt:=[2,2,1];

> readlib(exprofile):

> kernelopts(profile=true):

  writeto("output_add.txt");

  pt1:=pt:

  for i to 100 do

    pt1:=ec2[Add](pt1,pt)

  od:

  kernelopts(profile=false):

  writeto(terminal);

> excallgraph("output_add.txt");

                                                    used by Callee

    Caller                   Callee             #calls    time    words

    ======                   ======             ======    ====    =====

#++ <start>            calls Main_Routine           1, 105.223, 9608673

#++ Main_Routine       calls ec2[Add]             100,  20.110,  718473

#++ ec2[Add]           calls thirdpoint1          199,  14.563,  584687

#++ thirdpoint1        calls collect              199,  11.720,  410775

#++ collect            calls collect/recursive    200,   6.950,  344085

#++ collect/recursive  calls collect/series       200,   2.377,  256092

#++ ec2[Add]           calls reductionproc        100,   1.497,   77230

#++ ec2[Add]           calls isequal              200,   1.990,   31997

#++ collect/recursive  calls collect/recursive    400,   1.460,   31874

#++ collect            calls unknown              400,   1.380,   14048

#++ isequal            calls normalizationproc    203,    .670,    6365

#++ ec2[Add]           calls thirdpoint2            1,    .070,    3595

#++ thirdpoint2        calls collect                1,    .060,    2299

#++ collect/series     calls gc                     1,    .573,      65

#++ thirdpoint1        calls gc                     1,    .550,      65

#++ collect            calls gc                     1,    .527,      65

Le résultat affiché se comprend comme suit. La procédure principale a appelé ec2[Add] cent fois, ce qui ne nous étonne pas et le temps de calcul passé dans ec2[Add]est de 20.110s. La mémoire occupée par ce travail est de 718473 mots machine. La procédure ec2[Add] a appelé thirdpoint1 cent quatre-vingt-dix-neuf fois et thirdpoint2 une fois. Ceci est normal : au premier calcul de troisième point, on a deux points égaux ; ensuite ils sont distincts. De même on peut voir qu'à chaque appel de ec2[Add] la procédure isequal a été appelée deux fois.

Testons de même la soustraction.

> kernelopts(profile=true):

  writeto("output_subt.txt");

  pt1:=pt:

  for i to 100 do

    pt1:=ec2[Subt](pt1,pt)

  od:

  kernelopts(profile=false):

  writeto(terminal);

> excallgraph("output_subt.txt");

                                                    used by Callee

    Caller                   Callee             #calls    time    words

    ======                   ======             ======    ====    =====

#++ <start>            calls Main_Routine           1, 149.723,11638195

#++ Main_Routine       calls ec2[Subt]            100,  20.130,  729145

#++ ec2[Subt]          calls thirdpoint1          198,  14.633,  606596

#++ thirdpoint1        calls collect              198,  12.460,  460572

#++ collect            calls collect/recursive    199,   8.293,  398347

#++ collect/recursive  calls collect/series       199,   3.837,  316717

#++ ec2[Subt]          calls reductionproc        100,   1.427,   69345

#++ ec2[Subt]          calls isequal              200,   2.047,   31087

#++ collect/recursive  calls collect/recursive    398,   1.390,   30141

#++ collect            calls unknown              398,   1.257,   12733

#++ isequal            calls normalizationproc    205,    .597,    6240

#++ ec2[Subt]          calls thirdpoint2            1,    .063,    3048

#++ thirdpoint2        calls collect                1,    .050,    1939

#++ collect/series     calls gc                     3,   1.680,     198

Cette fois ci, on voit que les cent appels de ec2[Subt] ont pris 20.130s. Si l'on poursuit la comparaison, on se convainc qu'addition et soustraction ont vraiment des coûts similaires.

Pour bien comparer les deux méthodes, c'est-à-dire l'exponentiation binaire standard et la variante de Morain et Olivos, nous allons nous livrer à deux expériences. Pour la première exprérience nous reprenons les procédures ext1 et ext2 qui figure dans le code de EC et nous les modifions de manière qu'elles comptent les appels au doublement et à l'addition ou à la soustraction.

> ext1:=proc(n::posint)

    local L,i,a_counter,d_counter;

    a_counter:=0;

    d_counter:=0;

    L:=convert(n,base,2);

    for i to nops(L) do

      if L[i]=1 then a_counter:=a_counter+1 fi;

      d_counter:=d_counter+1

    od;

    [a_counter,d_counter]

  end:

> ext2:=proc(n::posint)

    local L,i,state,as_counter,d_counter;

    as_counter:=0;

    d_counter:=0;

    L:=convert(n,base,2);

    state:=0;

    for i to nops(L) do

      if L[i]=0 then 

        if state=0 then

          d_counter:=d_counter+1

        elif state=1 then

          as_counter:=as_counter+1;

          d_counter:=d_counter+2; 

          state:=0 

        else

          state:=1

        fi;

      else

        if state=0 then 

          state:=1

        else 

          if state=1 then

            as_counter:=as_counter+1;

            d_counter:=d_counter+1;

            state:=11

          fi;

          d_counter:=d_counter+1

        fi

      fi;

    od;

    as_counter:=as_counter+1;

    [as_counter,d_counter]

  end:

La procédure ext1 renvoie le couple nombre d'additions, nombre de doublements et la procédure ext2 renvoie le couple nombre d'additions ou soustractions, nombre de doublements. On espère que le deuxième a des composantes plus petites que le premier.

> ext1(10);

> ext2(10);

Nous effectuons la comparaison sur une large plage.

> nmin:=1:

  nmax:=1200:

> for n from nmin to nmax do 

    e1:=ext1(n);

    a1[n]:=e1[1];

    d1[n]:=e1[2];

    e2:=ext2(n);

    a2[n]:=e2[1];

    d2[n]:=e2[2] 

  od:

Ensuite nous représentons (en rouge) le nombre d'opérations dans l'exponentiation binaire (version additive) et (en noir) le nombre d'opérations dans la variante.

> picture[S1]:=plot([seq([n,a1[n]+d1[n]],n=nmin..nmax)],color=red):

> picture[S2]:=plot([seq([n,a2[n]+d2[n]],n=nmin..nmax)],

                                               color=black):

> plots[display]({seq(picture[i],i={S1,S2})});

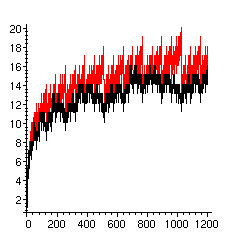
Il semble bien qu'il y ait toujours moins d'opérations dans la variante.

Passons à la seconde expérience. Il ne suffit pas que la théorie nous dise que la variante est meilleure. Peut-être n'avons nous pas pris en compte les bons paramètres. Nous reprenons la cubique favorite de Richard K. Guy, mais nous changeons de corps. Au lieu d'utiliser le corps des rationnels, nous employons un corps fini F_p où p est un nombre premier à cent chiffres décimaux. En effet il est implicitement supposé que les opérations dans le corps de base prennent un temps constant. Si nous travaillons avec des entiers comme plus haut, il va y avoir une croissance des nombres employés et les opérations de base vont être de plus en plus lentes. En bornant les nombres utilisés le problème est évacué.

Puisque nous employons maintenant un corps fini il nous faut une procédure de normalisation adaptée. La procédure de réduction n'est pas indispensable et à la réflexion elle est peut-être même nuisible.

> normalNproc:=proc(N::posint)

    local _N;

    subs(_N=N,

    proc(pt) 

      map(proc(expr) expr mod _N end,pt) 

    end)

  end:

> modNredproc:=proc(N::posint)

    local _N;

    subs(_N=N,

    proc(pt)

      local g,i,pt1; 

      pt1:=map(proc(expr) expr mod N end,pt);

      g:=igcd(op(pt1)); 

      if g=0 then ERROR() 

      else pt1:=[seq(pt1[i]/g,i=1..3)] 

      fi

    end)

  end:

> p:=nextprime(10^100);

> normalproc:=normalNproc(p):

> redproc:=modNredproc(p):

> ec3:=EC(f2,[x,y],[0,1,0],normalproc,redproc):

La cubique et les opérations qui lui sont associées étant définies, nous testons la multiplication externe du point usuel [2,2,1] par des entiers pris entre 1000 et 1100. On a pu constater plus haut, dans les résultats renvoyés par excallgraph, qu'un certain temps était employé par le ramasse-miettes gc. Pour éviter que ce temps ne soit comptabilisé dans les temps de calcul, nous faisons explicitement passer le ramasse-miettes avant chaque calcul. D'autre part nous notons les temps de calcul dans deux tables.

> nmin:=1000:

  nmax:=1100:

> for n from nmin to nmax do 

    gc():

    start:=time():

    pt2:=ec3[Ext1](n,pt):

    T1[n]:=time()-start;

    gc():

    start:=time():

    pt3:=ec3[Ext2](n,pt):

    T2[n]:=time()-start

  od:

Ensuite nous visualisons les temps de calcul et nous les comparons avec les nombres d'appels que nous avons calculés plus haut.

> plot([[seq([n,T1[n]],n=nmin..nmax)],

         [seq([n,T2[n]],n=nmin..nmax)]],color=[red,black]);

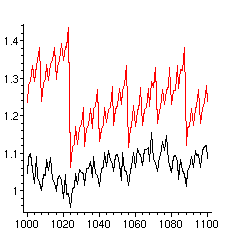
> plot([[seq([n,a1[n]+d1[n]],n=nmin..nmax)],

        [seq([n,a2[n]+d2[n]],n=nmin..nmax)]],color=[red,black]);

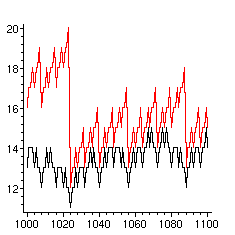
L'accord entre les deux graphes est frappant. Cela signifie que le nombre d'appels aux procédures d'addition, de soustraction et de doublement est le bon paramètre pour mesurer la complexité des deux procédures de calcul qui réalisent l'exponentiation binaire classique et sa variante. Ceci permet d'aborder une étude théorique qui est développée dans l'article de F. Morain et J. Olivos.

Pour en savoir plus sur les courbes elliptiques on pourra consulter [SiTa92]. Pour ce qui est de l'emploi de l'exponentiation binaire pour les calculs sur les courbes elliptiques, un complément est [KoTs92].

François Morain me fait remarquer que le contenu de l'article [MoOl90] peut être présenté plus simplement en employant la notion de NAF (abréviation de Non Adjacent Form, forme non adjacente), dont on trouvera une présentation dans le livre de Van Lint [vanLint92, sect. 10.2, page 135].

Retour en page principale