Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Programmation | Variantes

Programmation. La première question qui se pose est de parcourir la spirale. Nous écrivons donc une procédure sans grande finesse qui réalise ce parcours. Nous partons de l'origine. Ensuite l'action élémentaire consiste à faire le tour du carré obtenu à l'itération précédente. Pour cela nous procédons en quatre coups qui correspondent aux quatre bords du carré. Notez le positionnement du point courant pt avant chaque tour de carré (#). Au fur et à mesure, les points rencontrés sont rangés dans la table PT. En sortie nous renvoyons la séquence des points. Contrairement à ce que demande l'énoncé nous ne traçons pas la spirale. D'abord ceci permet de choisir les options de dessin les plus adéquates, ensuite on voit bien d'après la figure fournie page 108 et sa légende que les auteurs eux-mêmes ont procédé de cette façon puisqu'ils emploient un plot.

> ulam:=proc(n::nonnegint)

    local PT,pt,counter,i,direction,j;

    PT[1]:=[0,0]:

    pt:=[1,-1];                                       #

    counter:=1;

    for i to n do

      for direction in [[0,1],[-1,0],[0,-1],[1,0]] do

        for j to 2*i do

          pt:=[pt[1]+direction[1],pt[2]+direction[2]];

          counter:=counter+1;

          PT[counter]:=pt

        od

      od;

      pt:=[pt[1]+1,pt[2]-1]                           #

    od;

    [seq(PT[i],i=1..(2*n+1)^2)]

  end:

> ulam(3);

> plot(ulam(3),color=red,axes=boxed);

La procédure précédente n'est pas satisfaisante puisqu'on peut déterminer le numéro du point courant en employant les compteurs de boucle. La variable counter est donc inutile. Nous reprenons en modifiant légérement la procédure. Notez l'introduction de la procédure step pourvue d'une table de remember ( [GoSaZi95, exemple 22, page 43] ou [DuGo97, bas de la page 39]). On aurait pu tout aussi bien employer une table puisqu'on n'emploie essentiellement que la table de remember de cette procédure.

> ulam:=proc(n::nonnegint)

    local step,PT,pt,i,j,k;

    step(0):=[0,1];

    step(1):=[-1,0];

    step(2):=[0,-1];

    step(3):=[1,0];

    PT[1]:=[0,0];

    pt:=[1,-1];

    for i to n do

      for j from 0 to 3 do

        for k to 2*i do

          pt:=[pt[1]+step(j)[1],pt[2]+step(j)[2]];

          PT[(2*i-1)^2+j*2*i+k]:=pt;

        od

      od;

    pt:=[pt[1]+1,pt[2]-1] 

    od;

    [seq(PT[i],i=1..(2*n+1)^2)]

  end:

> ulam(3);

> plot(ulam(3),color=red,axes=boxed);

Pour obtenir la procédure demandée, il sufit maintenant de ne garder que les points associés à des nombres premiers. Nous réintroduisons donc un compteur, mais celui-ci n'est pas trivial comme le précédent. Il donne le nombre de nombres premiers plus petits que l'entier courant. Nous n'avons pas employé le crible d'Ératosthène, comme le suggérait l'énoncé. Le lecteur intéressé par cet algorithme pourra consulter [ DuGo97, page 121] (Voir aussi la page de commentaires de ce livre, au sujet du calcul de la fonction pi). Nous avons préféré employer la procédure isprime incluse dans le logiciel. Cette procédure emploie un algorithme probabiliste et le résultat n'est pas garanti. On pourrait obtenir la valeur true sur un entier non premier, mais les entiers que nous employons sont trop petits pour que cela pose problème.

> ulam:=proc(n::nonnegint)

    local step,PT,pt,i,j,k,counter;

    step(0):=[0,1];

    step(1):=[-1,0];

    step(2):=[0,-1];

    step(3):=[1,0];

    counter:=0;

    pt:=[1,-1];

    for i to n do

      for j from 0 to 3 do

        for k to 2*i do

          pt:=[pt[1]+step(j)[1],pt[2]+step(j)[2]];

          if isprime((2*i-1)^2+j*2*i+k) then

            counter:=counter+1;

            PT[counter]:=pt

          fi

        od

      od;

    pt:=[pt[1]+1,pt[2]-1] 

    od;

    [seq(PT[i],i=1..counter)]

  end:

> ulam(3);

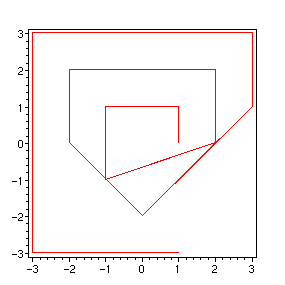
Un tracé brutal montre bien qu'il y eu sélection.

> plot(ulam(3),color=red,axes=boxed);

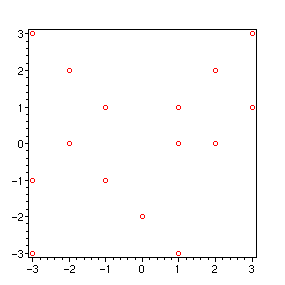
Approchons nous du dessin désiré.

> plot(ulam(3),color=red,style=point,symbol=circle,axes=boxed);

> plot(ulam(32),color=red,style=point,symbol=circle,axes=none);

> st:=time():

  plot(ulam(100),color=red,style=point,symbol=point,axes=none);

  time()-st;

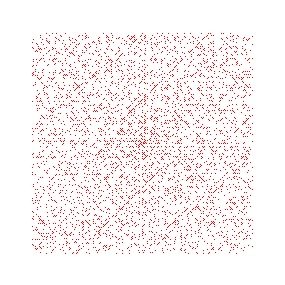
Variantes. La spirale d'Ulam est intriguante parce qu'on y distingue des alignements de points, qui semblent indiquer une certaine régularité dans la distribution des nombres premiers. Plus précisément, le fait d'avoir des points alignés signifie que l'on considère des valeurs entières d'un polynôme du second degré. Nous allons mettre ceci en valeur.

Nous avons besoin pour cela d'une procédure qui fournit les coordonnées du point de numéro n de la spirale. Pour cela nous plaçons l'entier n entre deux carrés impairs consécutifs, ce qui détermine un entier i tel que (2*i-3)^2 < n <= (2*i-1)^2. Ce i est le numéro du tour de spirale où se trouve le point associé à l'entier n. Ensuite nous déterminons l'entier k (égal à 0, 1, 2 ou 3) qui dit sur quel côté du carré se trouve le point de numéro n et son rang j sur ce côté. Le fait que le point numéro 1 soit l'origine n'aide pas à la clarté du code. On notera que cela fournit une nouvelle réponse à l'exercice posé (mais guère différente de la précédente).

> ulam:=proc(n::{posint,algebraic})

    local i,j,k;

    if type(n,posint) then

      for i from 0 while (2*i-1)^2<=n do od;

      if (2*i-3)^2=n then i:=i-1 fi;

      if i=1 then k:=0; j:=0 

      else

        k:=3-iquo((2*i-1)^2-n,2*(i-1),j);

        j:=2*i-j-2

      fi;

      i:=i-1;

      if k=0 then [i,-i+j]

      elif k=1 then [i-j,i]

      elif k=2 then [-i,i-j]

      else [-i+j,-i]

      fi

    else

      'ulam'(n)

    fi

  end:

> ulam(1);

Ensuite nous prenons un polynôme du second degré qui n'est pas quelconque. Il s'agit du polynôme d'Euler x^2+x+41. Il a la propriété de fournir des nombres premiers quand on substitue à x les entiers de 0 à 40. Nous calculons les points associés, puis nous les traçons.

> L:=[seq(ulam(x^2+x+41),x=0..40)]:

> plot(L,axes=boxed,style=point,symbol=cross,color=blue);

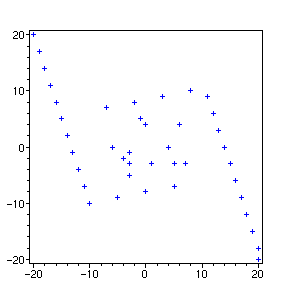
Comme nous l'avions annoncé, nous voyons bien surgir des alignements.

Nous reprenons avec un autre polynôme, découvert par R. Ruby, qui est similaire au polynôme d'Euler.

> L:=map(ulam,select(isprime,[seq(36*x^2-810*x+2753,

                                             x=-200..200)])):

> plot(L,axes=boxed,style=point,symbol=cross,color=blue);

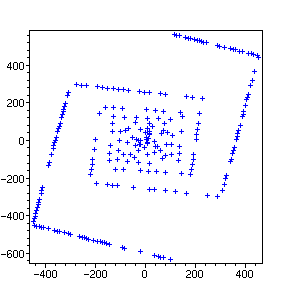
Ici encore nous voyons de jolis alignements. Au sujet des polynômes à coefficients entiers qui fournissent des nombres premiers sur un intervalle 0, 1, 2, ... assez long, on pourra consulter [ Ribenboim91, page 110 et suivantes].

On pourrait aussi repérer un alignement et se demander s'il est possible d'obtenir tout ou partie de ses points à travers les valeurs d'un polynôme du second degré.

Retour en page principale