Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

> x:=100;

> F:=add(z^(k^2),k=0..isqrt(x));

> series(F^2,z,x+1);

Nous voyons que les premiers sont 0, 1, 2, 4, 5, 8, 9, 10. Ils sont pondérés par le nombre de décompositions possibles. Par exemple 25 sécrit 25+0, 16+9, 9+16, 0+25 d'où le coefficient 4 qui figure devant z^25. Cependant la série obtenue n'est pas celle que nous voulons. Nous nous intéressons à la série support de celle-ci, obtenue en remplaçant un coefficient strictement positif par 1. Du coup la question ne ressortit plus à la notion de structure décomposable. Il convient de remplacer directement les coefficients strictement positifs par 1. C'est ce que nous faisons dans la procédure suivante.

> N:=proc(x::{numeric,name})

    local xx,F,z,S,P,counter,i,k;

    if type(x,name) then RETURN('N'(x)) fi;

    xx:=floor(x);

    F:=add(z^(k^2),k=0..isqrt(xx));

    S:=series(F^2,z,xx+1);

    P:=convert(S,polynom);

    counter:=0;

    for i from 0 to xx do

      if coeff(P,z,i)>0 then counter:=counter+1 fi

    od;

    counter

  end:

Nous avons ainsi réalisé la fonction N demandée.

> N(100.5);

> plot(N(t),t=0..100,scaling=constrained);

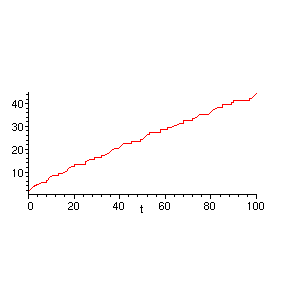
Nous tentons alors de faire apparaître le 0.764 promis par l'énoncé.

> for k to 10 do

    x:=2^k; 

    evalf(N(x)/(x/ln(x)^(1/2)))

  od;

La convergence est trop lente pour que nous constations le phénomène annoncé.

La question est trop subtile pour être abordée ainsi. Le théorème de Lagrange affirme que tout naturel est somme de quatre carrés. Quant aux entiers sommes de deux carrés, ils s'écrivent où est un entier et est un entier naturel produit de facteurs premiers distincts qui sont 2 ou un nombre premier congru à 1 modulo 4. Pour tout cela, on peut consulter [HaWr79, ch. XX] ou encore [Samuel71, ch. V]. Notons le nombre d'entiers naturels plus petits que et qui sont sommes de carrés mais pas de carrés. Alors , , et sont respectivement équivalents, quand tend vers l'infini, à ; avec où est le produit infini

dans lequel l'indice parcourt l'ensemble des nombres premiers congrus à 3 modulo 4; et enfin .

Revenons sur le nombre . En appliquant la formule ci-dessus, nous pouvons l'évaluer numériquement.

> pi:=1:

  p:=2:

  to 100 do

    p:=nextprime(p);

    if irem(p,4)=3 then pi:=pi*(1-1/p^2) fi

  od:

  b:=1/sqrt(2.*pi);

Nous retrouvons le 0.764 annoncé. Pour ces résultats, on peut consulter [Landau53, ch. LVIII, par. 183, pp. 668-669]. Pour un calcul efficace de la constante , on peut lire Zeta Function Expansions of Classical Constants (35kb), P. Flajolet and I. Vardi. Unpublished memo. February 1996. 10 pages. [uncompressed].

Retour en page principale