Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

La présentation donnée au paragraphe 3.2 de la réduction d'une forme quadratique n'est pas assez claire sur un point : la réduction n'est réellement possible (nous voulons dire algorithmique) que dans le cas de la dimension 2. En effet elle repose sur la détermination des valeurs propres d'une matrice symétrique réelle, c'est-à-dire sur la résolution d'une équation algébrique de degré n si la dimension vaut n. Or pour n plus grand que 4 on sait bien qu'il n'y pas d'expression par radicaux pour les racines et pour les degrés 3 et 4, les résultats renvoyés par le système emploient les formules de Cardan, qui peuvent faire intervenir des nombres complexes même si les racines sont réelles. Qui plus est, les procédures du package d'algèbre linéaire font apparaître des fonctions trigonométriques evaluées en des sous-mutliples d'arc tangente de nombres algébriques exprimés par radicaux. Pour les degrés 3 et 4, on se retrouve donc avec des expressions délicates à gérer et dans le cas général, on va être obligé d'employer un RootOf. On pourrait aborder la question en employant systématiquement RootOf, mais un autre problème surgit alors. La notation RootOf désigne l'une quelconque des racines d'un polynôme ; en fait c'est la racine que l'on obtient dans le quotient de l'anneau de polynômes par l'idéal généré par le polynôme. Or on veut disposer d'une ensemble de racines dans le corps des réels (ou plus généralement des complexes) qui sont la plupart du temps distinctes. Du coup cette notation, satisfaisante tant qu'on reste dans l'abstraction, ne convient plus pour gérer des racines dans un corps de nombres concret. Tout ceci fait que nous ne pouvons réellement traiter que le cas de la dimension 2. Pour les dimensions supérieures, il faudra que la chance soit avec nous pour que les racines cherchées s'expriment pas radicaux et d'une manière simple.

L'exercice recèle un petit piège ; en effet la matrice A n'est pas symétrique.

> A:=array(1..2,1..2,[[7/8,-sqrt(3)/4],[0,5/8]]);

> b:=array(1..2,1..1,[[2],[2*sqrt(3)]]);

> c:=7;

Ceci n'empêche pas de considérer la forme quadratique associée.

> X:=array(1..2,1..1,[[x],[y]]);

> Phi:=collect(evalm(transpose(X)&*A&*X+transpose(b)&*X+c)[1,1],

                                     {x,y},distributed);

La matrice utile est la partie symétrique de la matrice proposée. On peut la récupérer par la procédure de l'exercice précédent,

> dismantle(Phi,[x,y]);

> A1:=matrix([[7/8, -1/8*sqrt(3)], [-1/8*sqrt(3), 5/8]]);

ou tout simplement en explicitant ce qu'est la partie symétrique.

> evalm((transpose(A)+A)/2);

Ensuite nous procédons comme dans le texte. L'emploi de la réduction de Jordan est un peu troublante mais le cas est particulier : comme la matrice est symétrique réelle, nous savons d'avance qu'elle se diagonalise dans une base orthonormée.

> linalg[jordan](A1,P);

La matrice de passage P est orthogonale, mais pas orthonormée. Elle est orthogonale parce qu'il y a deux valeurs propres distinctes et les droites propres sont orthogonales.

> eval(P);

> tPP:=evalm(transpose(P) &* P);

Nous modifions la matrice de passage pour la rendre orthogonale. On notera qu'en dimension supérieure et si une valeur propre était multiple, les vecteurs propres pris dans le sous-espace propre associé, qui est de dimension au moins 2, ne seraient pas nécessairement orthogonaux. On pourrait (et devrait) alors employer le procédé de Schmidt.

> Q:=array(1..2,1..2,diagonal):

  Q[1,1]:=1/sqrt(tPP[1,1]):

  Q[2,2]:=1/sqrt(tPP[2,2]):

> P1:=evalm(P&*Q);

Nous vérifions que la nouvelle matrice est bien orthogonale.

> evalm(transpose(P1) &* P1);

Nous explicitons le changement de base en termes de coordonnées.

> newX:=array(1..2,1..1,[[newx],[newy]]);

> XX:=evalm(P1&*newX);

> tosubs1:={x=XX[1,1],y=XX[2,1]}:

Ceci nous permet de calculer la nouvelle expression de la fonction polynôme. Bien sûr la partie du second degré ne comporte plus de terme rectangle.

> newPhi:=collect(subs(tosubs1,Phi),{newx,newy},distributed);

Nous cherchons ensuite si la conique associée à la fonction polynôme a un centre. Nous pouvons faire le calcul dans les anciennes coordonnées.

> center:=solve({diff(Phi,x),diff(Phi,y)},{x,y});

Nous pouvons aussi l'effectuer avec les nouvelles coordonnées.

> newcenter:=solve({diff(newPhi,newx),diff(newPhi,newy)},

                                                {newx,newy});

La comparaison montre que cela revient au même.

> subs(newcenter,tosubs1);

Puisque la conique possède un unique centre, il s'agit d'une conique à centre et nous écrivons l'équation au centre.

> tosubs2:=subs(newxx=newx,newyy=newy,

            subs(newcenter,{newxx=xi+newx,newyy=eta+newy}));

> newnewPhi:=collect(subs(tosubs2,newPhi),{xi,eta},distributed);

Nous pouvons expliciter le changement de coordonnées global.

> tosubs:=subs(tosubs2,tosubs1);

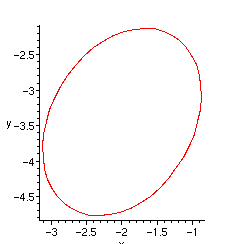
Disposant de l'équation réduite, il est facile de dessiner la conique, qui est ici une ellipse.

> arc:=subs(subs(xi=cos(t),eta=sqrt(2)*sin(t),tosubs),

                                         [x,y,t=0..2*Pi]);

> plot(arc,scaling=constrained,labels=[x,y]);

Retour en page principale