Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Nous employons la même méthode qu'à l'exercice 3 de la même page. Les problèmes évoqués dans l'introduction de cet exercice 3 vont nous compliquer un peu la tâche, mais l'énoncé est fait pour que les calculs aboutissent.

Pour saisir les données, nous pouvons définir la fonction polynomiale Phi et en tirer les matrices A et b et le nombre c (nous employons les notations de la page 138) grâce à la procédure de l'exercice 2 de la page 142, comme nous le faisons ci-dessous, ou bien définir les matrices et en tirer la fonction polynomiale.

> X:=array(1..2,1..1,[[x],[y]]);

> Phi:=7/8*x^2-3/8*x*y+sqrt(3)/8*x*z+23/32*y^2+3*sqrt(3)/16*y*z

                            +29/32*z^2-2*sqrt(3)*x+sqrt(3)*y-z+3;

> Dec:=dismantle(Phi,[x,y,z]);

> A:=Dec[1]:

> b:=Dec[2]:

> c:=Dec[3]:

Nous employons la réduction de Jordan pour obtenir la matrice diagonale semblable à la matrice A (nous savons qu'elle existe puisque la matrice A est symétrique réelle). Nous en tirons aussi une matrice de passage qui donne une base de vecteurs propres.

> linalg[jordan](A,P);

Les valeurs propres sont particulièrement simples. On sent que l'exemple a été bien choisi. Nous remarquons que l'une des valeurs propres est double.

> eval(P);

> tPP:=evalm(transpose(P) &* P);

> tPP:=map(radnormal,eval(tPP));

La base du plan propre associé à la valeur propre 1 n'est pas orthogonale. Nous faisons donc appel au procédé de Schmidt pour obtenir une base orthonormée. Pour cela nous explicitons la base dont nous disposons et le produit scalaire.

> for j to 3 do 

    f(j):=linalg[submatrix](P,1..3,j..j)

  od:

> scalarproduct:=proc(v,w)

    local i;

    add(v[i,1]*w[i,1],i=1..3)

  end:

Ensuite nous définissons la nouvelle base et noous construisons la matrice de passage associée.

> e(1):=map(radnormal,evalm(f(1)/sqrt(scalarproduct(f(1),f(1)))),

                                          rationalized):

> for j from 2 to 3 do

    s:=evalm(scalarproduct(e(1),f(j))*e(1));

    for k from 2 to j-1 do

      s:=evalm(s+scalarproduct(e(k),f(j))*e(k))

    od;

    e(j):=evalm(f(j)-s);

    e(j):=map(radnormal,evalm(e(j)/sqrt(scalarproduct(e(j),e(j)))),

                                                      rationalized)

  od:

> P1:=linalg[augment](seq(e(j),j=1..3));

> map(radnormal,evalm(transpose(P1) &* P1));

La nouvelle matrice de passage est bien une matrice orthogonale. On notera l'usage répété que nous faisons de radnormal. Rappelons que radnormal ramène à 0 toute quantité exprimée par radicaux et par les quatre opérations élémentaires à partir des entiers et qui est égale à zéro. Ensuite nous continuons le calcul comme dans l'exercice 3.

> newX:=array(1..3,1..1,[[newx],[newy],[newz]]);

> XX:=evalm(P1&*newX):

> tosubs1:={x=XX[1,1],y=XX[2,1],z=XX[3,1]}:

> newPhi:=map(radnormal,collect(subs(tosubs1,Phi),{newx,newy,newz},

                            distributed),rationalized);

L'expression de la fonction polynome du second degré dans la nouvelle base ne comporte plus de termes rectangles comme prévu. Nous cherchons si la quadrique possède un centre.

> center:=solve({diff(Phi,x),diff(Phi,y),diff(Phi,z)},{x,y,z});

> newcenter:=solve({diff(newPhi,newx),

                    diff(newPhi,newy),diff(newPhi,newz)},

                                              {newx,newy,newz});

> map(radnormal,subs(newcenter,tosubs1));

Nous avons trouvé un unique centre, donc nous avons affaire à une quadrique à centre. Le calcul a été effectué dans les anciennes et dans les nouvelles coordonnées. Le dernier résultat montre que les calculs sont cohérents. Cependant on aurait pu obtenir des écritures différentes car si radnormal fournit une forme normale (zéro ne s'écrit que 0) il ne fournit pas une forme canonique (un même nombre algébrique autre que zéro, exprimé par radicaux, peut avoir deux écritures distinctes fournies par radnormal).

Maintenant nous calculons l'équation au centre et aussi le changement de coordonnées qui fait passer des anciennes coordonnées aux coordonnées dans le dernier repère employé.

> tosubs2:=subs(newxx=newx,newyy=newy,newzz=newz,

             subs(newcenter,{newxx=xi+newx,newyy=eta+newy,

                                            newzz=zeta+newz}));

> newnewPhi:=map(radnormal,collect(subs(tosubs2,newPhi),

                          {xi,eta,zeta},distributed));

> tosubs:=map(radnormal,subs(tosubs2,tosubs1));

L'équation au centre montre que la quadrique est un ellipsoïde de révolution. On peut le tracer.

> surface:=subs(subs(xi=cos(phi)*sin(theta),

                     eta=sqrt(2)*sin(phi)*sin(theta),

                     zeta=cos(theta),tosubs),[x,y,z]);

> plot3d(surface,theta=0..Pi,phi=-Pi..Pi,scaling=constrained,

                               labels=[x,y,z],axes=boxed);

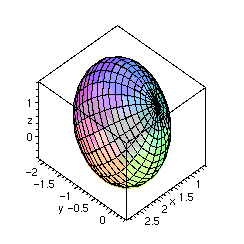
La forme réduite de la fonction polynomiale montre clairement que la valeur minimale qu'elle atteint est -1 et que cette valeur est atteinte en exactement un point qui est le centre de la quadrique. Quant au fait d'obtenir ce centre par deux calculs différents, je ne l'imagine pas et je n'en vois pas l'intérêt. Le calcul que nous avons fourni est la bonne manière d'aborder la question.

Retour en page principale