Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.3 worksheet Maple V.4 worksheet Maple V.5 worksheet

L'exercice est une application de la notion de base de Gröbner et en particulier de la notion d'élimination. On pourrait certes employer solve, comme il est indiqué dans l'énoncé, mais solve appelerait le package consacré aux bases de Gröbner. Autant donc éviter cette boîte noire qu'est solve. Nous traitons l'exercice d'abord en Maple V.3 puis en Maple V.5.

Traitement en Maple V.3 | Traitement en Maple V.5
Illustration | Addendum

Traitement en Maple V.3. Nous commençons par spécifier un système qui décrit algébriquement la situation géométrique. Pour cela nous choisissons comme origine le point A, comme axe des abscisses la droite AC et comme axe des ordonnées la droite AD. Ensuite nous exprimons successivement les faits suivants :

• les abscisses de A et D sont nulles ;
• les ordonnées de A, H et C sont nulles ;
• les points B et C d'une part, les points H et E d'autre part ont mêmes abscisses ;
• les points A, B et E d'une part, les points C, D et E d'autre part sont alignés ;
• les distances AB, DC, EH sont connues ;
• l'ordonnée de E vaut 1 (ce qui avec la condition de distance impose que AC et EH sont perpendiculaires --on pourrait aussi étudier le cas où l'ordonnée de E vaut -1, mais il suffit d'orienter l'axe des ordonnées dans l'autre sens et notre choix ne fait rien perdre) ;
• enfin l'ordonnée de B n'est pas nulle et les points A et C sont distincts (ce sont les conditions implicites du problème).

> 
sys:=[x[a],x[d],y[a],y[h],y[c],x[b]-x[c],x[h]-x[e],

    (x[b]-x[a])*(y[e]-y[a])-(y[b]-y[a])*(x[e]-x[a]),

    (x[c]-x[d])*(y[e]-y[d])-(y[c]-y[d])*(x[e]-x[d]),

    (x[b]-x[a])^2+(y[b]-y[a])^2-4,

    (x[d]-x[c])^2+(y[d]-y[c])^2-9,

    y[e]-1,1-t*x[b],(x[a]-x[c])^2+(y[a]-y[c])^2-u]:

Ensuite nous listons les indéterminées en jeu. L'ordre employé n'a pas beaucoup d'importance, sauf pour l'indéterminée x_c que nous plaçons en dernière position.

> 
var:=[t,u,x[a],x[d],y[a],y[c],y[h],y[e],

    x[b],y[b],y[d],x[h],x[e],x[c]];

Nous appliquons la procédure grobner[gbasis] avec l'option plex, c'est-à-dire que l'ordre employé pour ranger les monômes dans l'algorithme est l'ordre lexicographique avec x_c vue comme la plus petite indéterminée. Dans l'élimination des monômes de tête on élimine donc d'abord les autres indéterminées, ce qui a pour effet que la dernière équation du résultat ne comporte que l'indéterminée x_c.

> gb:=grobner[gbasis](sys,var,plex);

Comme indiqué page 158, le système obtenu est triangulaire. Pour mettre ceci en valeur, nous associons à la base de Gröbner une matrice. Chaque ligne de la matrice correspond à un polynôme de la base ; chaque colonne de la matrice correspond à une indéterminée. De plus nous respectons l'ordre de la base et des indéterminées. Le coefficient d'indice (i,j) de la matrice vaut 1 si la variable d'indice j figure dans le polynôme d'indice i et 0 sinon.

> G:=array(1..nops(gb),1..nops(var),sparse):

  for i to nops(gb) do

    for j to nops(var) do

      if has(gb[i],var[j]) then G[i,j]:=1 fi

    od

  od:

  print(G);

Le caractère triangulaire est frappant. La forme de la matrice est à comparer à celle de la matrice que l'on obtient en appliquant le même calcul au système de départ.

> S:=array(1..nops(gb),1..nops(var),sparse):

  for i to nops(gb) do

    for j to nops(var) do

      if has(sys[i],var[j]) then S[i,j]:=1 fi

    od

  od:

  print(S);

L'équation qui nous intéresse particulièrement est celle qui correspond au dernier polynôme de la base.

> equ1:=subs(x[c]=z,gb[nops(gb)]);

À ce point on pourrait faire appel à fsolve par l'instruction suivante.

> fsolve(equ1,z);

Mais si l'on veut rester dans l'esprit du calcul formel et obtenir des résultats garantis, la bonne voie est celle des suites de Sturm.

> readlib(sturm);

> sturmseq(equ1,z);

> sturm(sturmseq(equ1,z),z,0,infinity);

Nous constatons que l'équation possède exactement deux solutions positives. Bien sûr, nous pourrions raffiner en procédant par dichotomie (avec des intervalles d'extrémités rationnelles) pour encadrer les racines. Par exemple, nous constatons qu'une des racines est entre 12/10 et 13/10.

> sturm(sturmseq(equ1,z),z,12/10,13/10);

On aurait aussi pu essayer la résolution exacte par solve, mais outre que ceci ne fonctionne généralement pas, dans le cas présent les résultats sont inutilisables. On pourra s'en convaincre par les instructions suivantes. En V.3, allvalues renvoie des valeurs flottantes ; par contre avec V.5, on obtient des expressions avec radicaux qui découle des formules de Ferrari et qui sont surtout énormes.

> solve(equ1,z);

> equ2:=subs(z=w^(1/2),equ1);

> solve(equ2,w);

> allvalues(");

Passons à la version V.5.

Traitement en Maple V.5. Pour la version V.5, le calcul des bases de Gröbner a été complètement revu et Frédéric Chyzak a écrit un nouveau package Groebner qui remplace l'ancien package grobner (encore disponible dans cette version). Les possibilités de ce nouveau package sont considérablement supérieures à celles de l'ancien. Les ordres de termes sont maintenant au choix de l'utilisateur (?Groebner,termorder) et les indéterminées ne sont plus nécessairement commutatives, ce qui permet de traiter des problèmes liés à des opérateurs linéaires (?Ore_algebra).

Reprenons la séquence de calcul, en l'adaptant à à la nouvelle syntaxe. On notera en particulier que var est ici une séquence et non une liste.

> sys:={x[a],x[d],y[a],y[h],y[c],x[b]-x[c],x[h]-x[e],

  (x[b]-x[a])*(y[e]-y[a])-(y[b]-y[a])*(x[e]-x[a]),

  (x[c]-x[d])*(y[e]-y[d])-(y[c]-y[d])*(x[e]-x[d]),

  (x[b]-x[a])^2+(y[b]-y[a])^2-4,

  (x[d]-x[c])^2+(y[d]-y[c])^2-9,

  y[e]-1,1-t*x[b],(x[a]-x[c])^2+(y[a]-y[c])^2-u}:

> var:=t,u,x[a],x[d],y[a],y[c],y[h],y[e],

  x[b],y[b],y[d],x[h],x[e],x[c];

> gb:=Groebner[gbasis](sys,plex(var));

On note qu'avec cette nouvelle syntaxe, c'est la première équation de la base qui nous importe.

> G:=array(1..nops(gb),1..nops([var]),sparse):

  for i to nops(gb) do

    for j to nops([var]) do

      if has(gb[i],var[j]) then G[i,j]:=1 fi

    od

  od:

  print(G);

Pour s'initier aux bases de Gröbner, on peut lire [BeWe93], qui ne suppose pas de connaissances particulières autres qu'une certaine familiarité avec l'algèbre.

Illustration. Pour conclure, mous allons illustrer la question géométrique en dessinant les deux configurations obtenues. Dans ce but, nous calculons en flottants les deux solutions réelles positives annoncées.

> fsol:=[fsolve(gb[1],x[c])];

> fsol:=select(proc(x) x>0 end,fsol); 

Pour chacune d'elles, nous calculons le jeu de valeurs associées. Ceci se fait sans problème car le système est linéaire en les autres variables. Pour effectuer le calcul, nous évacuons l'équation où ne figure que x_c ; nous résolvons le système ; nous rajoutons l'égalité qui donne la valeur de x_c.

> for i to nops(fsol) do

    Fsol[i]:=fsolve(select(has,{op(subs(x[c]=fsol[i],gb))},{var}),

                    {var} minus {x[c]})

             union {x[c]=fsol[i]}

  od;

Ensuite nous réalisons un dessin qui est constitué de deux parties : les noms des points et les segments. Les segments dont les longueurs ont été imposées par l'énoncé sont en gras.

> for i to 2 do

    text:=plots[textplot](subs(Fsol[i],{

              [x[a]-.1,y[a]-.1,"A"],

              [x[b],y[b]+.2,"B"],

              [x[c]+.1,y[c]-.1,"C"],

              [x[d]-.1,y[d],"D"],

              [x[e],y[e]+.2,"E"],

              [x[h],y[h]-.1,"H"]})):

    picture:=plot(subs(Fsol[i],[

              [[x[a],y[a]],[x[c],y[c]]],

              [[x[a],y[a]],[x[d],y[d]]],

              [[x[a],y[a]],[x[b],y[b]]],

              [[x[c],y[c]],[x[d],y[d]]],

              [[x[e],y[e]],[x[h],y[h]]],

              [[x[c],y[c]],[x[b],y[b]]],

              [[x[a],y[a]],[x[h],y[h]]],

              [[x[h],y[h]],[x[c],y[c]]],

              [[x[a],y[a]],[x[e],y[e]]],

              [[x[b],y[b]],[x[e],y[e]]],

              [[x[c],y[c]],[x[e],y[e]]],

              [[x[e],y[e]],[x[d],y[d]]]]),

              thickness=[1,1,3,3,3,1,1,1,1,1,1,1],

              color=black):

   figure[i]:=plots[display]({text,picture},axes=none)

  od:

> for i to 2 do figure[i] od;

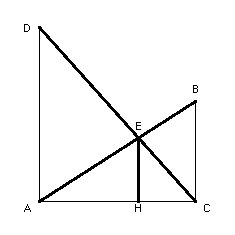
Nous laissons le lecteur tester la séquence d'instructions suivantes, où l'on n'a pas ajouté les conditions implicites signalées dans l'énoncé.

> sys:={x[a],x[d],y[a],y[h],y[c],x[b]-x[c],x[h]-x[e],

  (x[b]-x[a])*(y[e]-y[a])-(y[b]-y[a])*(x[e]-x[a]),

  (x[c]-x[d])*(y[e]-y[d])-(y[c]-y[d])*(x[e]-x[d]),

  (x[b]-x[a])^2+(y[b]-y[a])^2-4,

  (x[d]-x[c])^2+(y[d]-y[c])^2-9,

  y[e]-1}:

> var:=t,u,x[a],x[d],y[a],y[c],y[h],y[e],

  x[b],y[b],y[d],x[h],x[e],x[c]:

> gb:=Groebner[gbasis](sys,plex(var));

Addendum. Bruno Salvy me fait remarquer que le théorème de Thalès permet de se ramener à un système en deux indéterminées et d'employer le résultant.

Retour en page principale