Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.3 worksheet Maple V.4 worksheet Maple V.5 worksheet

Calcul en Maple V.3 | Notion de base de Gröbner
Calcul pas à pas

Avant tout, il faut noter que l'énoncé est faux. La surface d'équation x^2+y^2=z/2 n'est pas un cône mais un paraboloïde elliptique. Le dessin de la figure VI.9 correspond plutôt au cône d'équation x^2+y^2=z^2. Nous ne tenons donc compte que des équations en négligeant le dessin.

Calcul en Maple V.3. Nous appliquons la méthode présentée dans l'exemple 27, page 163, et nous employons le package grobner de la version V.3.

> sys:={x^2+y^2-z/2,(y-1)^2+(z+4)^2-1};

> gbxy:=grobner[gbasis](sys,[z,x,y],plex);

> gbxz:=grobner[gbasis](sys,[y,x,z],plex);

> gbyz:=grobner[gbasis](sys,[x,y,z],plex);

Dans chaque cas, la seconde des deux équations, celle qui ne fait plus apparaître la première indéterminée pour l'ordre choisi, donne la plus petite variété contenant la projection sur le plan de coordonnées des deux dernières indéterminées, et ceci est un résultat général. Pour xOy et xOz on voit apparaître des quartiques, c'est-à-dire des courbes du quatrième degré. Pour yOz, on voit réapparaître l'intersection du cylindre et du plan de coordonnées.

Yann Blanchard remarque, en s'appuyant sur la formule

17y^2-2y+16+16x^2+4x^4+8x^2y^2+4y^4=4(x^2+y^2)^2+16(x^2+y^2)+(y-1)^2+15,

que l'intersection considérée est vide si le corps de base est le corps des réels. En effet le membre gauche de l'égalité est le membre gauche de l'une des équations (nous écrivons toujours les équations sous la forme P=0) que nous avons obtenues en considérant la projection sur xOy. Du coup on peut se demander ce que signifie la locution la plus petite variété contenant la projection sur le plan de coordonnées. Elle n'a de sens précis que si l'on indique le corps dans lequel sont résolus les systèmes algébriques. Des résultats intéressants apparaissent si l'on travaille avec la clôture algébrique du corps des coefficients des polynômes qui définissent l'idéal. En effet dans ce cadre, un idéal détermine une variété algébrique et inversement la variété algébrique détermine un idéal qui est le radical du précédent. Autrement dit, on alors une correspondance bijective entre les variétés algébriques et les idéaux radicaux. Si le corps n'est pas algébriquement clos, la considération de la variété ne permet généralement pas de retrouver l'idéal et est donc inadéquate. Par exemple ici, le fait de constater que cette intersection est vide du point de vue réel ne permet pas de comprendre ce que sont les polynômes obtenus.

Notion de base de Gröbner. La présentation qui est donnée des bases de Gröbner (section 2.1) est assez superficielle, pour ne pas effrayer le lecteur. Nous allons essayer d'être un peu plus précis dans cette page.

La donnée du calcul est un ensemble de polynômes en plusieurs indéterminées. Ces polynômes engendrent un idéal dans l'anneau des polynômes sur un corps donné, ici le corps des rationnels. On veut disposer d'une procédure de décision qui permette de dire si un polynôme donné appartient à l'idéal. Plus généralement on voudrait que la procédure réduise un polynôme donné modulo l'idéal et que le résidu soit obtenu sous une forme unique. Dans le cas des polynômes en une indéterminée tout ceci est fourni par la division euclidienne.

Dans le cas des polynômes en une indéterminée, un ordre naturel sur les monômes est le suivant : plus le degré d'un monôme est grand et plus ce monôme est grand pour l'ordre considéré. Pour les polynômes en plusieurs indéterminées, il n'y a pas d'ordre naturel et unique sur les monômes. Il faut introduire explicitement un ordre, plus complexe que dans le cas d'une indéterminée. Dans l'exemple précédent, on a utilisé l'ordre lexicographique (décrit page 156).

La construction de la procédure de décision désiré s'appuie sur la considération des termes de tête des polynômes. Le terme de tête d'un polynôme est son plus grand monôme, pour l'ordre qui a été fixé. Pour développer une bonne intuition, nous nous restreignons à travailler avec deux indéterminées x et y. Chaque polynôme de l'idéal possède un terme de tête x^ay^b. Nous considérons tous les points (a,b) à coordonnées entières ainsi obtenus. Si un point (a,b) est associé à un polynôme P de l'idéal, alors les points (a+1,b) et (a,b+1) sont aussi associés à des polynômes de l'idéal comme on le voit en considérant xP et yP. Du coup la frontière de l'ensemble des points (a,b) est un escalier, qui a l'allure suivante.

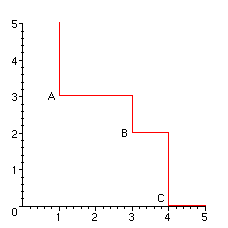
Les points A, B, C déterminent complètement l'escalier. Ce sont ces points distingués que l'on veut déterminer et plus précisément pour chacun de ces points un polynôme de l'idéal.

Chaque point distingué détermine un quart de plan nord-est. Si un polynôme de l'idéal donne un terme de tête qui est au dessus de l'escalier, alors ce terme de tête est dans le quart de plan nord-est associé à un point distingué et on peut le réduire en lui soustrayant un multiple convenable du polynôme associé au point distingué. Ainsi tout polynôme de l'idéal sera ramené sous l'escalier, c'est-à-dire nécessairement au polynôme nul.

La question est de savoir comment déterminer les points distingués et des polynômes associés. Au départ, on dispose d'un ensemble de générateurs dont les termes de tête déterminent certains points du plan sans propriétés particulières. Considérons par exemple une paire de deux générateurs P₁ et P₂ dont les termes de tête sont x⁴y et x²y³, ce qui donne les deux points (4,1) et (2,3). Il est alors assez naturel de considérer le polynôme y²P₁-x²P₂. S'il n'y avait pas de simplification, le terme de tête serait x⁴y³. Grâce au choix des coefficients y² et x², on va obtenir un terme plus petit et donc se rapprocher de l'escalier associé à l'idéal.

Calcul pas à pas. Nous revenons à l'exercice proposé pour montrer comment se déroule le calcul et nous employons le package Groebner de la version V.5. Nous considérons les deux polynômes du système (nous avons évacué le dénominateur 2 pour simplifier). Comme il y a trois indéterminées, l'escalier devient tridimensionnel.

> P[1]:=-2*(x^2+y^2-z/2):

  P[2]:=(y-1)^2+(z+4)^2-1:

Nous étudions la paire constituée de ces deux polynômes. Nous calculons les monômes dominants des deux polynômes pour l'ordre choisi. Ce sont les seconds éléments de chacune des deux séquences renvoyées ci-dessous.

> Groebner[leadmon](P[1],plex(z,x,y));

> Groebner[leadmon](P[2],plex(z,x,y));

Comme z est l'indéterminé la plus grande, nous récoltons comme monômes dominants les monômes en z de plus grand degré. Nous constatons que les points (0,0,1) et (0,0,2) sont associés à des polynômes de l'idéal. Nous employons le ppcm des deux monômes pour tenter de fabriquer un polynôme dont le terme de tête est plus petit au regard de l'ordre choisi.

> collect(z*P[1]-P[2],[z,x,y],distributed);

C'est exactement ce que fait la procédure Groebner[spoly].

> S[1,2]:=Groebner[spoly](P[1],P[2],plex(z,x,y));

Nous réduisons maintenant le polynôme S_1,2 en employant P₁ et P₂. Pour cela nous regardons à chaque fois le monôme dominant pour l'ordre choisi.

> Groebner[leadmon](S[1,2],plex(z,x,y));

> P[3]:=collect(S[1,2]+2*x^2*P[1],[z,x,y],distributed);

> P[3]:=collect(P[3]+2*y^2*P[1],[z,x,y],distributed);

> P[3]:=collect(P[3]+8*P[1],[z,x,y],distributed);

> P[3]:=-P[3];

À ce stade, nous ne pouvons plus appliquer de réduction. Le résultat obtenu est fourni par la procédure Groebner[reduce].

> Groebner[reduce](S[1,2],[P[1],P[2]],plex(z,x,y));

Nous reprenons maintenant la même technique avec P₁ et P₃.

> Groebner[leadmon](P[1],plex(z,x,y));

> Groebner[leadmon](P[3],plex(z,x,y));

> collect(x^4*P[1]-z*P[3],[z,x,y],distributed);

> S[1,3]:=Groebner[spoly](P[1],P[3],plex(z,x,y));

Nous pourrions continuer le calcul pas à pas, mais les deux termes de tête de P₁ et P₃ ne partagent pas d'indéterminées. Il en résulte que S_1,2 peut être réduit à zéro en employant P₁ et P₃. C'est bien ce que renvoie Groebner[reduce].

> Groebner[reduce](S[1,3],[P[1],P[3]],plex(z,x,y));

La situation est la même pour P₂ et P₃.

> S[2,3]:=Groebner[spoly](P[2],P[3],plex(z,x,y));

> Groebner[reduce](S[2,3],[P[2],P[3]],plex(z,x,y));

Du coup nous n'avons pas créé de nouveau polynôme, ce qui termine cette phase de calcul. On a ainsi obtenu l'escalier cherché. Il est la frontière de la réunion des huitièmes d'espace associés aux trois polynômes. Cependant on constate facilement qu'il y a redondance, car le huitième d'espace associé à P₂ est dans celui associé à P₁. On termine donc par une phase de réduction où chacun des polynômes est réduit par rapport aux autres.

> Groebner[inter_reduce]([seq(P[i],i=1..3)],plex(z,x,y));

Ce que l'on a obtenu au bout du compte est appelé une base de Gröbner de l'idéal.

Retour en page principale