Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

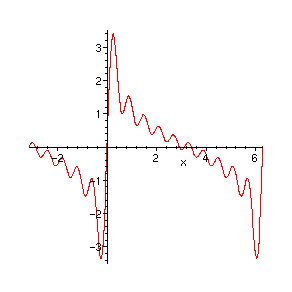
Commençons par tracer les graphes de quelques sommes partielles.

> N:=10:

  S:=add(sin(n*x)/sqrt(n),n=1..N):

> plot(S,x=-Pi..2*Pi,numpoints=500);

> N:=20:

  S:=add(sin(n*x)/sqrt(n),n=1..N):

> plot(S,x=-Pi..2*Pi,numpoints=500);

  N:='N':

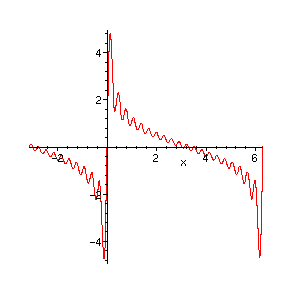
Tant que la variable reste dans un segment qui ne contient pas de multiple de Pi, la série semble converger sans problème. En employant la transformation d'Abel ou directement le théorème d'Abel, on prouverait aisément qu'il y a convergence uniforme dans un tel segment.

Il reste à étudier le comportement de la série au voisinage de multiples de Pi et pratiquement dans un voisinage à droite de zéro, vues les symétries. En fait nous allons étudier le comportement de la somme quand la variable tend vers zéro par valeurs positives. Nous allons voir que la fonction somme a une limite infinie en zéro et il n'y a donc pas convergence uniforme. Le résultat que nous allons obtenir sera bien plus précis.

Pour cela nous employons la méthode de Kummer. Elle consiste à remplacer le terme géral d'une série convergente par un terme équivalent que l'on sait sommer. Ceci induit bien sûr une différence, mais cette différence converge plus vite vers zéro. Ici les coefficients binomiaux sont de bons candidats parce que nous voyons le terme général de la série comme la partie imaginaire de et nous voulons employer la formule du binôme

> u0:=convert(binomial(-1/2,n),GAMMA);

> asympt(u0,n,3);

> da0:=map(expand,map(combine,%,power,symbolic),trig);

Nous voyons que le binomial d'indices -1/2 et n se comporte en 1/sqrt(n). Nous allons chercher un développement de 1/sqrt(n) suivant l'échelle, inusuelle mais adaptée à la situation, des binomial(k-1/2,n). Nous disposons de asympt qui nous donne des développements dans l'échelle usuelle des puissances de n. Nous effectuons donc les calculs avec des coefficients indéterminés puis nous résolvons. Cela revient à inverser la matrice qui fait passer d'une échelle à l'autre.

> kmax:=3;

> dev:=sqrt(Pi)*add(c[k]*binomial(k-1/2,n),k=0..kmax);

Nous ajoutons 2 à la variable kmax pour ajuster le nombre d'inconnues et le nombre d'equations.

> asympt(1/sqrt(n)-dev,n,kmax+2);

> da:=map(combine,%,power,symbolic);

Nous effectuons un petit bricolage pour récupérer les équations qui nous intéressent.

> daL:=convert(da,set):

> sys:=map(select,has,daL,c);

> sys:=map(convert,sys,set):

> sys:=map(subs(cc=c,proc(s) op(select(has,s,cc)) end),sys);

> inc:={seq(c[k],k=0..kmax)};

> C:=solve(sys,inc);

Ayant déterminé les solutions, il n'y a plus qu'à substituer dans l'expression du développement suivant les binomiaux.

> DEV:=subs(subs(cos(Pi*n)=1/(-1)^n,C),dev):

> DEV:=expand(DEV);

Le développement ne comporte pas de terme d'erreur. Il suffirait de pousser le calcul d'un cran supplémentaire pour voir qu'il s'agit d'un O(binomial(7/2,n)) ou d'un O(n^(-9/2)).

En faisant preuve d'un optimisme béat, nous tentons la sommation.

> sum(DEV*sin(n*x),n=1..infinity);

Cela ne produit rien. Nous en venons donc explicitement à ce que nous avions en tête, à savoir la formule du binôme.

> DA:=map(proc(expr) sum(expr*z^n,n=1..infinity) end,DEV);

Ensuite nous remplaçons z par exp(I*x) et nous contrôlons de près le logiciel pour arriver à l'expression qui nous intéresse. Nous obtenons ainsi la substitution à effectuer pour passer de l'expression en z à l'expression en x.

> assume(sin(2*theta)>0):

> for expr in DA do

    tosubs[expr]:=subs(theta=x/4,

         simplify(evalc(Im(subs(

                        toto=(1-I)*exp(I*theta)*sin(2*theta)^(1/2),

                        z=exp(I*4*theta),

         simplify(subs(1-z=toto^2,expr),radical,symbolic))))))

  od;

Précisément, il suffirait d'employer l'instruction suivante pour obtenir l'expression en x. Mais cela n'est guère intéressant car les contributions des différents termes sont mélangées.

> niceDA:=subs(seq(expr=tosubs[expr],expr=DA),DA):

Il est plus instructif de tracer le graphe associé à chaque terme.

> for expr in DA do

    plot(tosubs[expr],x=0..Pi,view=[0..Pi,-5..5])

  od;

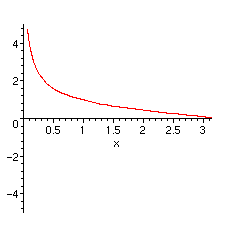
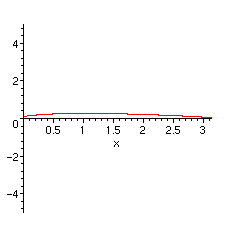
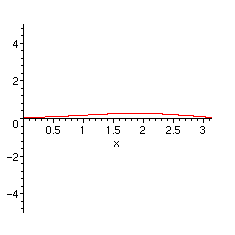
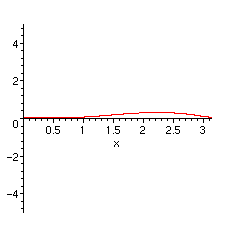
Nous voyons bien que le premier graphe donne l'allure essentielle de la somme de la série, qui apparaissait dans les graphes que nous avons tracés au début. Ensuite les contributions sont de plus en plus faibles et les fonctions de plus en plus lisses. Si l'on se place du point de vue de l'analyse complexe, il n'est pas difficile de justifier le calcul. Les fonctions en z qui apparaissent sont analytiques dans le plan complexe privé de la demi-droite réelle de 1 à l'infini. Leurs développements en série entière en zéro a un rayon de convergence égal à 1. Essentiellement les termes du développement que nous avons obtenu font apparaître les fonctions (1-z)^(-1/2), (1-z)^(1/2), (1-z)^(3/2), etc. La substitution de exp(I*x) à z revient à considérer ces fonctions sur le cercle unité. Seule la première a une limite infinie au point 1 et les suivantes ont des comportements de plus en plus lisses (sans être toutefois développables en série entière au point 1). C'est donc la première qui donne le comportement essentiel de la fonction somme de la série.

Si l'on ne connaît que l'analyse réelle la question est plus compliquée. On voit bien toutefois que le premier terme donne le comportement essentiel de la fonction somme. En effet le deuxième terme du développement asymptotique donne une série normalement convergente, puisqu'on a un O(n^(-3/2)), et la somme est une fonction continue. Le troisième terme donne une série qui est non seulement normalement convergente mais dont la série formellement dérivée est aussi normalement convergente donc la fonction somme est de classe C^1. Le problème est de déterminer le comportement du premier terme. Le logiciel a permis de dégrossir la question puisqu'on voit maintenant le but à atteindre. On peut tenter de prouver une formule exacte, compagne de la formule du binôme inaccessible à cause de la présence d'une racine carrée de nombre complexe, mais au vu du résultat obtenu ci-dessus cela semble difficile, ou une formule asymptotique en 1/sqrt(x) comme celle que fournit le calcul suivant.

> for expr in DA do

    series(tosubs[expr],x)

  od;

On trouvera dans le livre d'Antoni Zygmund [Zygmund88, sections II.13 et V.2] une étude du comportement dans le voisinage de zéro des sommes des séries sum(n^(-beta)*cos(n*x),n=1..infinity) et sum(n^(-beta)*sin(n*x),n=1..infinity) pour 0<beta<1.

Retour en page principale