Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

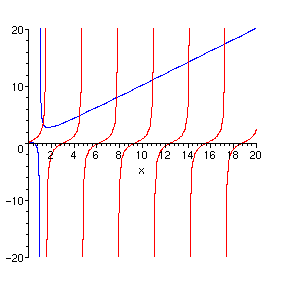
L'exercice est tout à fait similaire à l'exemple traité page 208. Un argument de continuité couplé avec un argument de monotonie montre qu'il y a exactement une solution dans chaque intervalle ]n*Pi,n*Pi+ Pi/2[. On peut illustrer la situation par le dessin suivant.

> plot([tan(x),x^3/(x^2-1)],x=0..20,color=[red,blue],

                     discont=true,view=[0..20,-20..20]);

Dans le cas traité en exemple, x=tan(x), on pose t=2/Pi/(2*n+1), x=1/t-u et on obtient l'équation x=1/t-u=tan(Pi/2-u). Elle est du premier degré en t et elle se résout en t=1/(u+tan(Pi/2-u)), ce qui permet ensuite d'employer series et solve. Ici une petite difficulté surgit, parce que l'équation n'est pas du premier degré en t. Nous posons toujours t=2/Pi/(2*n+1), x=1/t-u, mais l'équation est 1/z=tan(Pi/2-u) avec z=x^3/(x^2-1). Remarquons que t, u et z sont proches de 0. Pour essayer de clarifier la situation nous notons U, T, X des expressions qui représentent des développements asymptotiques respectivement de u, t, x. Nous fixons la valeur de la variable d'environnement Order qui va déterminer la précision des développements obtenus.

> Order:=10:

Nous exprimons d'abord u en fonction de z. À dire vrai, le calcul n'est guère utile car nous connaissons le résultat par coeur. Nous l'effectuons dans un souci de généralité.

> U:=solve(z=series(tan(u),u),u);

Ensuite nous exprimons z en fonction de x et x en fonction de t et u, de manière à revenir à la situation de l'exemple.

> U:=subs(z=subs(x=1/t-u,(x^2-1)/x^3),U);

Nous développons u par rapport à t. Nous obtenons un développement à coefficients en u. Bien sûr nous voudrions un développement qui ne soit fonction que de t. Nous effectuons donc un aller-retour.

> U:=series(U,t);

> T:=solve(u=U,t);

> U:=solve(t=T,u);

Maintenant nous exprimons x=1/t-u en fonction de n et nous développons en fonction de n.

> X:=subs(u=U,t=2/Pi/(2*n+1),1/t-u);

> X:=asympt(X,n);

Si l'on veut un développement plus précis il suffit d'augmenter Order et de reparcourir la séquence d'instructions.

Nous pouvons tester sur un exemple la qualité du développement.

> nn:=10;

> evalf(eval(subs(O=0,n=nn,X)));

> fsolve(x^3/(x^2-1)=tan(x),x=nn*Pi..nn*Pi+Pi/2);

Retour en page principale