Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

L'énoncé parle de développement en série, ce qui pourrait faire penser que la variable x est proche de 0 et que l'on cherche un développement en série entière. En fait on va voir que l'on travaille pour x grand et que l'on fournit un développement asymptotique suivant les puissances de 1/x.

Les termes de la série vont d'abord en croissant puis décroissent. Pour déterminer (approximativement) l'entier qui donne le maximum, nous calculons le rapport r de deux termes consétifs et nous résolvons asymptotiquement l'équation r=1.

> u:=(Pi/2)^(2*n+1)/(2*n+1)!/(4*n+3)*x^(4*n+3);

> r:=simplify(convert(subs(n=n+1,u)/u,GAMMA),GAMMA);

> r:=combine(r,power,symbolic);

Nous fixons la valeur de la variable d'environnement Order, ce qui va déterminer la précision du résultat.

> Order:=10:

Nous définissons z=1/n, pour calculer au voisinage de 0. L'équation r=1 s'écrit plus précisément s(n)*x^4=1. Nous calculons le développement asymptotique du coefficient s(n).

> s:=series(subs(n=1/z,r/x^4),z);

Ce développement commence par un terme en z^2. Comme il est expliqué page 207, il vaut mieux imposer un terme du premier degré. Nous récrivons donc l'équation sous la forme s(n)^(1/2)=1/x^2. De plus comme x tend vers l'infini quand n tend vers l'infini, nous passons par t=1/x^2.

> da:=subs(t=1/x^2,series(1/solve(series(s^(1/2),z)=t,z),t));

Testons le résultat pour la valeur x=3, comme évoqué pages 196-198.

> xx:=3;

> evalf(eval(subs(O=0,x=xx,da)));

> plot([seq([i,subs(x=xx,n=i,u)],i=0..10)]);

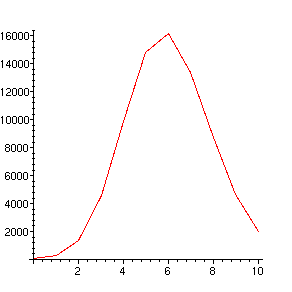
Nous obtenons 5.3 alors que la bonne valeur est 6. Ce n'est pas formidable, mais 3 n'est pas bien grand. Essayons plutôt avec x=10.

> xx:=10;

> evalf(eval(subs(O=0,x=xx,da)));

> plot([seq([i,subs(x=xx,n=i,u)],i=0..100)]);

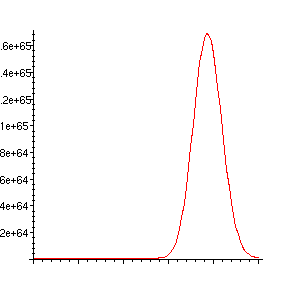
Comme nous ne distinguons pas l'indice qui donne le maximum à l'oeil nu, nous le calculons en parcourant l'intervalle de 71 à 90.

> i0:=70:

  m:=[i0,evalf(subs(x=xx,n=i0,u))]:

  for i from i0+1 to i0+20 do

    v:=evalf(subs(x=xx,n=i,u));

    if v>m[2] then m:=[i,v] fi

  od:

  m;

La valeur obtenue est 76.8 et l'entier le plus proche est la bonne valeur. Ce n'est pas mal.

Retour en page principale