Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Calcul du développement | Comparaison numérique
Recherche d'une forme explicite

Calcul du développement.< Fixons x dans l'intervalle ouvert ]-1,1[. Alors x sin^2(t) reste dans un segment de l'intervalle ]-1,1[. Sur ce segment la série entière développement de ln(1+u) converge normalement et donc aussi la série obtenue en développant ln(1+x sin^2(t)). On peut donc l'intégrer terme à terme, ce qui donne le développement en série entière

en notant F(x) la fonction considérée et w_n l'intégrale de Wallis. Celle-ci (que l'on connaît bien) peut être calculée par le logiciel.

> int(sin(t)^(2*n),t=0..Pi/2);

Une application brutale de series suffit à fournir le développement demandé.

> series(Int(ln(1+x*sin(t)^2),t=0..Pi/2),x);

Comparaison numérique. Comparons le développement et la fonction. Nous définissons la fonction et les coefficients du développement. Ensuite nous traçons les graphes des troncatures du développement et le graphe de la fonction.

> F:=Int(ln(1+x*sin(t)^2),t=0..Pi/2);

> nnmax:=10:

> for nn to nnmax do w[nn]:=int(sin(t)^(2*nn),t=0..Pi/2) od:

> s:=0:

  for nn to nnmax do

    s:=s+(-1)^(nn-1)*w[nn]/nn*x^nn;

    pic[nn]:=plot(s,x=-1.05..1.05,view=[-1..1,-1..1],color=black)

  od:

> pic[infinity]:=plot(F,x=-0.95..0.95,view=[-1..1,-1..1],

                                                       color=red):

> plots[display]({pic[infinity]});

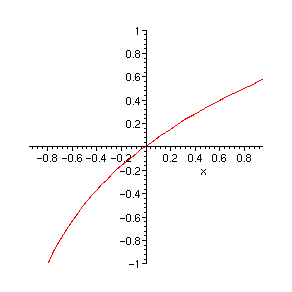
> plots[display]({seq(pic[nn],nn=1..nnmax),pic[infinity]});

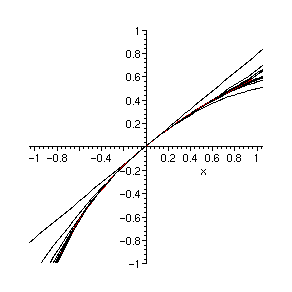
Pour x positif le développement est une série alternée et la valeur absolue du terme général décroît à partir d'un certain rang qui dépend de x. On peut donc lui appliquer le critère de Leibniz sur les séries alternées (à partir d'un certain rang). Ceci se manifeste par le fait que les graphes des troncatures encadrent le graphe de la fonction (à partir d'un certain rang).

On nous demandait de comparer les valeurs en x=1/10.

> evalf(subs(x=1/10,s));

> evalf(subs(x=1/10,F));

Recherche d'une forme explicite. On peut se demander si l'intégrale ne possède pas une forme explicite. Il n'est pas difficile de prouver que l'on peut dériver sous le signe somme.

> F1:=Int(diff(op(1,F),x),op(2,F));

Tentons donc d'évaluer la dérivée.

> F1:=value(F1);

Nous obtenons une expression explicite, qu'il est tentant d'intégrer.

> int(F1,x);

Le logiciel échoue, mais nous remarquons qu'interviennent partout les nombres x et 1+x et leurs racines carrées. Il est donc normal de spécifier le cas x=ch(theta)^2, qui devrait permettre des simplifications.

> G:=int(ln(1+cosh(theta)^2*sin(t)^2),t=0..Pi/2);

Nous obtenons une expression explicite. Cependant ceci est une illusion car le dilogarithme est définie à l'aide d'une intégrale ou d'une série. Disons que nous sommes revenus à un cas de base. Nous voyons aussi que cette expression explicite ne nous fournit rien de mieux que l'expression intégrale de la fonction ou que son développement en série.

Retour en page principale