Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Les conditions imposées aux entiers n et i se traduisent par les trois conditions suivantes : on peut écrire n=i*q+r ; l'entier r est entre 0 et n (strictement pour ce dernier) ; le quotient r/i est plus grand que 1/2. Autrement dit le reste dans la division euclidienne de n par i est supérieur ou égal au quotient de i par 2.

Ceci nous permet le test suivant. Nous marquons les couples (n,i) qui satisfont la condition imposée.

> nmax:=100:

> counter:=0:

  for n to nmax do

    for i to n do

      if irem(n,i)>=iquo(i,2) then

        counter:=counter+1;

        T[counter]:=[n,i]

      fi

    od

  od:

  n:='n':

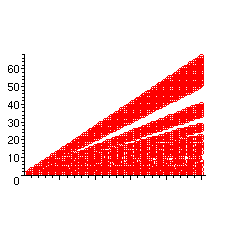
> plot([seq(T[c],c=1..counter)],style=point,symbol=circle,

                             color=red,scaling=constrained);

Le dessin met en valeur le fait que les couples (n,i) sont ceux tels que le rapport i/n appartienne à une réunion d'intervalles. C'est ici que l'on pourrait introduire une somme de Riemann, comme suggéré par l'énoncé, en considérant la fonction caractéristique de cette réunion d'intervalles.

Dire que le couple (n,i) satisfait la bonne condition c'est dire que l'on peut écrire 1/(q+1) <= n/i < 1/(q+1/2) pour un entier q entre 1 et n. Le nombre des entiers i qui satisfont cette paire d'inégalités, pour n donné, vaut donc environ n/(q+1/2)-n/(q+1). On doit ensuite sommer ces nombres pour q allant de 1 à n. Mais les nombres 1/(q+1/2)-1/(q+1) donnent une série convergente. On a donc une bonne approximation en prenant la somme de la série multipliée par n. Les deux approximations que nous venons de faire correspondent au passage à la limite dans la somme de Riemann évoquée par le texte.

> K:=sum(1/(q+1/2)-1/(q+1),q=1..infinity);

> evalf(K);

La constante K est la proportion d'entiers i qui satisfont la condition pour un n donné. Nous pouvons tester numériquement ce résultat.

> ntest:=1000:

  counter:=0:

  for i to ntest do

    if irem(ntest,i)>=iquo(i,2) then

      counter:=counter+1

    fi

  od:

> evalf(counter/ntest);

N'est ce pas splendide ?

Retour en page principale