Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Équation de point fixe | Singularités
Développement asymptotique de la fonction
Développement asymptotique du coefficient

Commençons par la mauvaise voie, c'est-à-dire la résolution brutale, irréfléchie et sans finesse. Il suffit de tester les commandes suivantes pour comprendre qu'elles ne mènent pas loin.

> S:=[solve(equ,w)];

> for f in S do series(f,z) od;

Il est même étonnant que l'on obtienne une réponse car l'équation algébrique est du cinquième degré. On va bientôt voir pourquoi. Quoi qu'il en soit le résultat est inutilisable.

Équation de point fixe. Passons aux choses sérieuses. Tout d'abord l'énoncé est passablement approximatif, voir faux. La question ne porte pas sur une fonction T(z), mais sur une série formelle en z. En effet l'équation proposée est une équation de point fixe dans l'algèbre des séries formelles et le membre droit fournit une application contractante (au sens de la métrique usuelle des séries formelles, qui fait que les monômes de grand degré sont proches de la série formelle nulle). Cela résulte de la présence des termes z et z^2 en facteur de T(z) et T(z)^5. Comme à chaque fois que l'on peut appliquer le théorème du point fixe, on approche la solution par itération. C'est ce qui est fait dans les instructions suivantes, qui fournissent les dix premiers termes de la série formelle.

> t:=1:

  for nn to 10 do

    t:=series(subs(w=t,1+z*w^2+z^2*w^5),z,nn+1)

  od:

  t;

On note au passage que la positivité des coefficients du membre droit de l'équation définissant T(z) se traduit par la positivité des coefficients de T(z).

L'équation qui définit T(z) est une équation algébrique. Regardons la de plus près.

> equ:=w-(1+z*w^2+z^2*w^5);

> factor(equ);

L'équation n'est pas irréductible, ce qui n'est pas usuel dans un exercice. La série T(z) n'est certainement pas racine du premier facteur car on obtiendrait une racine carrée de z ce qui n'existe pas dans l'algèbre des séries formelles. C'est donc l'autre facteur qui nous intéresse.

> equ1:=select(has,%,w^3);

Nous pouvons vérifier que l'approximation de la série que nous avons obtenu plus haut satisfait bien (et approximativement) cette nouvelle équation.

> series(subs(w=t,equ1),z,nn);

Par contre on note que cette équation est plus compliquée que la précédente du point de vue des séries formelles, car le théorème du point fixe ne s'y applique pas. Il n'est pas aussi évident qu'elle détermine exactement une série formelle en z (mais il suffit d'employer le théorème de Lagrange [ Comtet70, tome premier, page 159] pour s'en convaincre).

Singularités. Comme il est expliqué à la page 222, le comportement des coefficients de la série formelle T(z) passe par l'étude de la fonction T(z) et particulièrement de ses points singuliers. On notera qu'il y a là une petite entourloupe car rien ne dit que la série entière T(z) définit bien une fonction. Ou plutôt, il faudrait être plus savant. Nous reviendrons bientôt là-dessus. Les points singuliers d'une fonction algébrique s'obtiennent en écrivant que le théorème des fonctions implicites ne s'applique pas. Si l'équation s'écrit P(z,w)=0 et que l'on veut résoudre en w, on doit donc chercher les points (z,w), qui annulent à la fois le polynôme P et sa dérivée par rapport à w. On peut donc démarrer le calcul comme suit.

> dequ1:=diff(equ1,w);

On forme l'équation aux abscisses en éliminant w par un calcul de résultant.

> R:=resultant(equ1,dequ1,w);

> factor(R);

> singabs:={solve(R,z)};

On a ainsi les abscisses possibles des points singuliers. Cependant, il faut ensuite remettre ces abscisses dans l'équation P(z,w)=0 pour obtenir les ordonnées. Cela n'est pas une bonne idée car l'équation est du troisième degré en w. Il vaut mieux former l'équation aux ordonnées car l'équation n'est que du premier degré en z.

> R:=resultant(equ1,dequ1,z);

> factor(R);

> singord:={solve(R,w)};

Disposant des ordonnées possibles, il ne reste plus qu'à chercher les abscisses correspondantes.

> for yy in singord do

    Z[yy]:=[solve(subs(w=yy,equ),z)];

    if Z[yy]<>[] then

      s[yy]:=seq([x,yy],x=Z[yy])

    else s[yy]:=NULL

    fi

  od:

  singpt:=[seq(s[yy],yy=singord)];

On a ainsi trouvé les points singuliers. Ils sont réels. D'après le texte de la page 222, on doit chercher celui (ou ceux) dont l'absisse est la plus proche de l'origine . Clairement c'est le deuxième qui convient.

> nearest:=singpt[2];

La situation est plus compliquée que peut le laisser penser le texte de la page 122. En fait la notion de point le plus proche est délicate. La singularité qui convient n'est pas nécessairement celle de plus petit module, parce que la fonction algébrique est définie sur une surface de Riemann et l'origine et le point singulier apparemment le plus proche pourrait être sur des feuillets différents ; du coup un point singulier apparemment plus éloigné pourrait être le point utile. On comprend que les auteurs n'aient pas voulu entrer dans ces subtilités. Ici la situation est particulière car la série entière est à coefficients positifs. Le théorème de Pringsheim permet d'affirmer que la singularité la plus proche est sur l'axe réel positif. Il n'y a donc pas à hésiter : c'est 4/27 qui convient.

Développement asymptotique de la fonction. Nous étudions maintenant l'équation (réduite) au voisinage du point singulier en effectuant une translation du repère.

> equ1;

> equ2:=collect(subs(z=4/27-z1,w=3/2+w1,equ1),{z1,w1},distributed);

Nous avons écrit z=4/27-z1 et non pas z=4/27+z1 parce que nous avons en tête d'aller de l'origine au point singulier.

Dans l'exemple traité, il était évident que l'on attendait un développement en sqrt(alpha-z) parce que l'on considérait une équation du second degré. Ici l'équation est du troisième degré. Pour déterminer les exposants possibles nous dessinons le polygone de Newton de la courbe algébrique pour le point singulier considéré. Cela consiste à marquer les points (n,m) dans le quart de plan des couples d'entiers positifs si le monôme z1^n*w1^m apparaît dans l'équation que nous venons d'obtenir.

> for i in equ2 do

    N[i]:=[degree(i,z1),degree(i,w1)] 

  od:

> plot([seq(N[i],i=equ2)],style=point,symbol=circle,color=red);

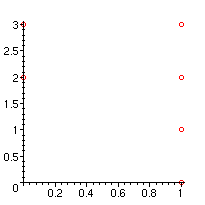
Ensuite on regarde les pentes des segments qui joignent les points deux à deux et qui sont sous le nuage de points. Ici il n'y a qu'une segment qui apparaît, celui qui joint (0,2) et (1,0), et sa pente est -1/2. Il en résulte que le développement cherché va s'écrire suivant les puissance de z1^(1/2). Pour une justification, nous renvoyons à [Dieudonne80, page 106]. Expliquons simplement l'idée de base. Si nous posons w1=z1^mu, en reportant dans l'équation nous avons un polynôme en z1 et le monôme z1^n*w1^m fournit un monôme z1^(n+mu*m) (l'exposant n'est a priori plus un entier). Puisque l'équation exprime que ce nouveau pseudo-polynôme est nul, il faut bien que des annulations se produisent. Précisément on exprime que les termes qui fournissent les puissances les plus petites disparaissent et cela suppose une égalité de la forme n_1+mu*m_1=n_2+mu*m_2. C'est ce qui fait apparaître les segments joignant les points et leurs pentes.

La considération du polygone de Newton n'est pas indispensable pour l'exemple qui nous occupe. En effet l'instruction suivante nous montre de manière plus elémentaire que 4/27-z se comporte en (w-3/2)^2 au voisinage du point singulier. Cette simplification tient au fait que l'équation est du premier degré en z.

> series((w-1)/w^3,w=3/2);

L'exposant à considérer est donc 1/2. Pour simplifier la gestion des expressions nous introduisons Z1=z1^2. Ainsi tous les exposants sont entiers. On cherche le développement local par coefficients indéterminées. Nous pourrions procéder par étapes comme à la page 224 ou dans l'exercice 1, page 212, mais cela n'est pas satisfaisant car on transforme des indéterminées en variables informatiques, ce qui fait que la séquence de calcul n'est pas réexécutable.

> equ3:=subs(z1=Z1^2,equ2):

> imax:=5:

> W1:=add(a[i]*Z1^i,i=1..imax);

> localequ:=series(subs(w1=W1,equ3),Z1,imax+1);

> localequ:=convert(localequ,polynom):

> sys:={seq(coeff(localequ,Z1,i),i=2..imax)}:

  inc:={seq(a[i],i=1..imax-1)}:

> SOL:=[solve(sys,inc)];

Nous obtenons deux solutions, ce qui est normal à cause de l'extraction de racine carrée. Celle qui convient est la seconde parce que la fonction croît entre 0 et 4/27 et on attend donc un coefficient négatif en facteur de sqrt(4/27-z1).

> localw:=3/2+subs(SOL[2],a[imax]*Z1^imax=O(Z1^imax),Z1=z1^(1/2),

                                                         W1);

Développement asymptotique du coefficient. Nous opérons la substitution qui correspond à la formule (9) de la page 222.

> subs(seq((z1)^(i+1/2)=

        (4/27)^(i+1/2)*GAMMA(n-i-1/2)/GAMMA(-i-1/2)

                            /factorial(n)/(4/27)^n,

                         i=0..iquo(imax,2)),localw);

Les termes qui comportent des puissances entières positives de z1=4/27-z ne nous intéressent pas car ils ne participent qu'à un nombre fini de coefficients et n'ont donc pas à intervenir dans le développement asymptotique des coefficients. Nous les évacuons et nous tentons de passer dans une échelle usuelle.

> da:=select(has,%,n);

> da:=map(asympt,da,n);

Error, (in asympt) unable to compute series

Reprenons en ne substituant pas une expression en gamma mais directement le développement asymptotique de cette expression.

> da:=(27/4)^n*select(has,

      subs(seq((z1)^(i+1/2)=(4/27)^(i+1/2)

        *asympt(GAMMA(n-i-1/2)/GAMMA(-i-1/2)/factorial(n),n),

               i=0..iquo(imax,2)),localw),n):

> da:=combine(da,exp):

> da:=map(asympt,da,n);

Nous obtenons le résultat cherché. Testons numériquement ce développement. Nous calculons l'approximation qu'il nous donne du centième coefficient de la série formelle T(z).

> subs(O=0,n=100,da):

> evalf(%);

D'autre part nous reprenons la séquence de calcul vue au début pour obtenir exactement ce centième coefficient.

> t:=1:

  for nn to 100 do

    t:=series(subs(w=t,1+z*w^2+z^2*w^5),z,nn+1)

  od:

  coeff(convert(t,polynom),z,100);

> evalf(%);

La comparaison est tout à fait satisfaisante.

Avec un petit effort supplémentaire, le lecteur n'aura pas de mal à modifier la séquence de calcul pour qu'elle produise un développement suivant l'échelle des (27/4)^n/n^(k/2) avec une précision fixée à l'avance.

Retour en page principale