Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

1 | 2
Comparaison V.4-V.5

Nous traitons d'abord les deux questions en employant Maple V.5.

1. Résolution en cartésiennes. Évidemment la fonction nulle est solution. Le logiciel nous fournit les solutions suivantes.

> deq:=(x+y(x)*diff(y(x),x))^2-x^2-y(x)^2;

> sol:={dsolve(deq,y(x))};

Évacuons la solution nulle et récrivons les autres solutions.

> Sol:=remove(has,sol,0);

> for i to nops(Sol) do

    Y[i]:=normal(subs(Sol[i],y(x)))

  od;

Nous avons des solutions opposées deux à deux, ce qui est évident dès qu'on regarde l'équation. Le cas où la constante _C1 est nulle donne la solution nulle. Nous pouvons donc supposer qu'elle est non nulle. Les solutions non nulles sont fournies par les expressions suivantes. Attention, les Y[1] et Y[2] ci-dessous ne sont pas ceux qui figurent ci-dessus. Nous disons simplement que les deux ensembles des fonctions associées sont les mêmes.

> Y[1]:=-2*_C1*sqrt(1-x/_C1);

> Y[2]:=2*_C1*sqrt(1-x/_C1);

Les graphes des solutions maximales associées à ces expressions sont des demi-paraboles.

> plot(subs(_C1=1,Y[1]),x=-2..1);

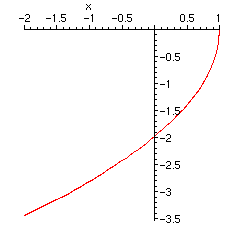
> plot(subs(_C1=1,Y[2]),x=-2..1);

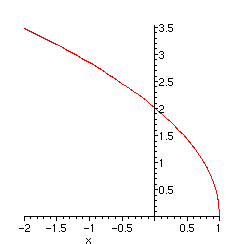
Représentons quelques courbes intégrales.

> kmax:=5:

> xmin:=-8:

  xmax:=8:

> plot({[x,0,x=xmin..xmax],

      seq(subs(_C1=-k,[x,Y[1],x=_C1..xmax]),k=1..kmax),

      seq(subs(_C1=k,[x,Y[1],x=xmin.._C1]),k=1..kmax),

      seq(subs(_C1=-k,[x,Y[2],x=_C1..xmax]),k=1..kmax),

      seq(subs(_C1=k,[x,Y[2],x=xmin.._C1]),k=1..kmax)},

                                                 color=red);

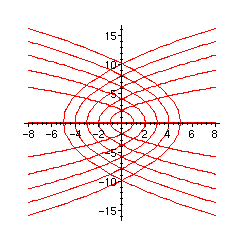
Pour ce qui est de la résolution, nous voyons que par chaque point qui n'est pas sur l'axe des abscisses il passe deux courbes intégrales. La solution nulle définie sur toute la droite réelle est une solution maximale. Les autres solutions maximales sont définies sur des demi-droites ouvertes.

Résolution en polaires. La forme de l'équation amène à rechercher une solution qui s'exprime en coordonnées polaires. Cette méthode fonctionne bien parce que l'équation est une équation différentielle homogène et l'équation transformée est à variables séparables. Nous procédons au changement de variables.

> polardeq:=DEtools[Dchangevar]({x=rho(theta)*cos(theta),

                               y(x)=rho(theta)*sin(theta)},

                                                    deq,x,theta);

Ensuite nous tentons la résolution et nous aidons le logiciel à nous donner des expressions utilisables.

> polarsol:={dsolve(polardeq,rho(theta))};

> polarSol:=select(has,polarsol,tan):

> for i to nops(polarSol) do

    Rho[i]:=combine(convert(subs(polarSol[i],rho(theta)),ln),

                                                  ln,symbolic)

  od;

> for i to nops(polarSol) do 

    Rho2[i]:=simplify(subs(1+tan(theta)^2=1/cos(theta)^2,

                           tan(theta)=sin(theta)/cos(theta),

                           normal(Rho[i]^2)),

                      radical,symbolic)

  od;

Comme plus haut nous jouons sur l'aspect arbitraire des constantes pour récrire l'ensemble des solutions sous une forme plus simple à manipuler.

> Rho[1]:=_C1/(1+cos(theta));

> Rho[2]:=_C1/(1-cos(theta));

Nous reconnaissons dans ces expressions des paramétrages de paraboles.

> plot(subs(_C1=1,Rho[1]),theta=-Pi..Pi,coords=polar,

                                view=[-2..2,-2..2]);

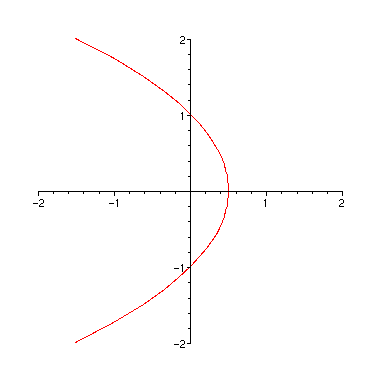
> plot(subs(_C1=1,Rho[2]),theta=-Pi..Pi,coords=polar,

                                view=[-2..2,-2..2]);

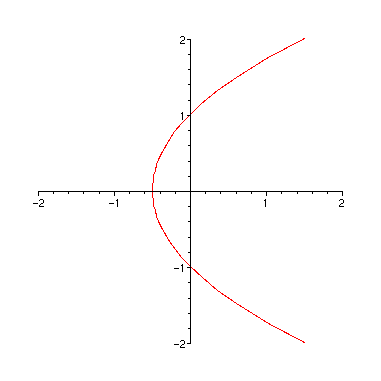
Le passage en polaires a fait perdre la solution nulle puisque nous cherchions des arcs paramétrés par l'angle polaire. D'autre part, ce calcul ne fournit pas des solutions de l'équation différenetielle proposée mais des solutions d'un problème plus général où l'on cherche comme solutions des arcs paramétrés. Pour obtenir des solutions au problème de départ, il faut découper ces arcs en morceaux qui sont des graphes de fonctions dérivables.

2. Nous explicitons l'équation, qui admet de manière évidente l'identité et son opposée comme solution.

> deq:=(x*diff(y(x),x)-y(x))^2-(x^2-y(x)^2);

Nous demandons la résolution.

> sol:={dsolve(deq,y(x))};

> for i to nops(sol) do

    Y[i]:=subs(sol[i],y(x))

  od;

Nous dessinons quelques graphes des solutions que nous venons d'obtenir.

> plot([seq(subs(_C1=k,Y[1]),k=-5..5)],x=0.1..3,

         view=[0..3,-3..3],

         color=[seq(COLOR(RGB,1/2-k/10,0,1/2+k/10),k=-5..5)]);

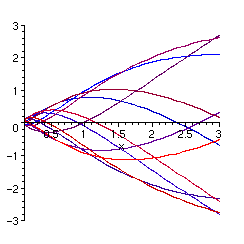
Aucune des solutions fournies par le logiciel n'admet un prolongement dérivable en zéro.

L'équation fournie est homogène. Cela est bien visible si on la récrit

.

Pour la résoudre, on cherche d'abord les solutions linéaires. On trouve ainsi les deux solutions x->x et x->-x, définies sur toute la droite réelle, que nous avons remarquées dès le début. Ensuite on procède à un changement de fonction inconnue . Ceci suppose de travailler dans un intervalle qui ne contient pas zéro. On fait ainsi apparaître une équation à variables séparables

.

La résolution de cette équation donne les solutions fournies par le logiciel.

Finalement les solutions maximales sont les deux solutions linéaires définies sur toute la droite réelle ; les solutions définies à droite de zéro par les expressions renvoyées par Maple ; les solutions définies à gauche de zéro par les mêmes expressions où l'on a changé x en -x.

Comparaison V.4-V.5. Le traitement de cet exercice est laborieux en Maple V.4 et les instructions que nous avons employées en Maple V.5 passent mal en V.4. Reprenons d'abord la première question.

> deq:=(x+y(x)*diff(y(x),x))^2-x^2-y(x)^2;

> sol:={dsolve(deq,y(x))};

La résolution a fourni x en fonction de y et non l'inverse (sauf pour la solution nulle). De plus les expressions comportent trop de radicaux et l'argument tangente hyperbolique est un logarithme qui est ensuite composé avec une exponentielle. Il faut simplifier tout cela.

> Sol:=remove(has,sol,0);

> for i to nops(Sol) do

  X[i]:=simplify(

          rationalize(

            normal(

              expand(

               combine(

                 convert(

                   simplify(subs(Sol[i],x),radical,symbolic),

                   ln),                #convert

                 ln,symbolic)^2

                    )              #expand

                  )              #normal

                     )^(1/2),

          radical,symbolic)  #simplify

  od;

Les expressions sont maintenant suffisamment simples pour que la résolution en y fonctionne.

> for i to nops(Sol) do

    Y[i]:=solve(X[i]=x,y(x))

  od;

Les expressions ne sont pas les mêmes qu'en V.5, mais on a qualitativement le même résultat.

> Y[1]:=-_C1*sqrt(1+2*x/_C1);

> Y[2]:=_C1*sqrt(1+2*x/_C1);

> kmax:=5:

> xmin:=-8:

  xmax:=8:

> plot({[x,0,x=xmin..xmax],

    seq(subs(_C1=-k,[x,Y[1],x=xmin..-_C1/2]),k=1..kmax),

    seq(subs(_C1=k,[x,Y[1],x=-_C1/2..xmax]),k=1..kmax),

    seq(subs(_C1=-k,[x,Y[2],x=xmin..-_C1/2]),k=1..kmax),

    seq(subs(_C1=k,[x,Y[2],x=-_C1/2..xmax]),k=1..kmax)},

                                               color=red);

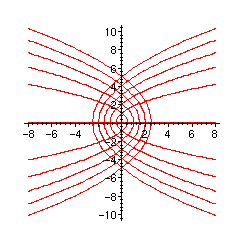
Pour ce qui est du passage en polaires, il semble que ce soit une impasse.

> polardeq:=DEtools[Dchangevar]({x=rho(theta)*cos(theta),

                               y(x)=rho(theta)*sin(theta)},

                                                    deq,x,theta);

> polarsol:={dsolve(polardeq,rho(theta))};

Error, (in dsolve/diffeq/genhomo) division by zero

Voyons l'autre question.

> deq:=(x*diff(y(x),x)-y(x))^2-(x^2-y(x)^2);

> sol:={dsolve(deq,y(x))};

À nouveau la résolution fournit x en fonction de y et non l'inverse. De plus des simplifications sont nécessaires pour disposer d'expressions utilisables.

> for i to nops(sol) do

    X[i]:=simplify(subs(sol[i],x),radical,symbolic)

  od;

On peut se battre un peu avec le logiciel.

> for i to nops(sol) do

    X[i]:=convert(X[i],exp)

  od;

> for i to nops(sol) do

    X[i]:=combine(X[i],exp)

  od;

> for i to nops(sol) do

    X[i]:=combine(X[i],ln,symbolic)

  od;

Mais ce bricolage est bien lassant. Il vaut mieux revenir à la méthode de résolution des équations homogènes. On cherche d'abord les solutions linéaires.

> factor(eval(subs(y(x)=C*x,deq)));

On voit bien apparaître les deux solutions x->x et x->-x. Ensuite on change de fonction inconnue.

> auxdeq:=DEtools[Dchangevar](y(x)=t(x)*x,deq,x);

> dsolve(auxdeq,t(x));

On n'a pas exactement ce qui convient mais au moins il est possible de gérer la crise et de deviner ce que sont les solutions.

Finalement on voit que la résolution des équations différentielles a été nettement améliorée de la version V.4 à la version V.5.

Retour en page principale