Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.3 worksheet Maple V.4 worksheet Maple V.5 worksheet

1 | 2

1. L'exercice comporte deux questions. Abordons la première de manière brutale, d'abord en V.3 puis en V.5.

> eq:=abs(x)*diff(y(x),x)+(x-1)*y(x)=x^2;

> dsolve(eq,y(x));

> eq:=abs(x)*diff(y(x),x)+(x-1)*y(x)=x^2;

> dsolve(eq,y(x));

On note une petite différence de comportement entre les deux versions. Cela n'a guère d'importance car cette voie est mauvaise. Il convient de discuter suivant le signe de la variable et donc de considérer deux équations.

> `eq+`:=x*diff(y(x),x)+(x-1)*y(x)=x^2;

> dsolve(`eq+`,y(x));

> `Y+`:=subs(%,y(x)):

> `eq-`:=-x*diff(y(x),x)+(x-1)*y(x)=x^2;

> dsolve(`eq-`,y(x));

> `Y-`:=subs(%,y(x)):

Les conditions du théorème de Cauchy-Lispchitz (cas linéaire) sont réunies quand on emploie l'un des deux intervalles ]-infinity,0[ ou ]0,+infinity[. Nous constatons bien que dans chaque cas, l'espace des solutions est de dimension 1.

Il convient maintenant d'étudier le comportement au voisinage de zéro. Une solution définie au voisinage de zéro coïncide avec un Y+ dans un voisinage à droite de zéro et avec un Y- dans un voisinage à gauche de zéro. Nous regardons donc le comportement de ces fonctions au voisinage de zéro.

> series(`Y+`,x);

> series(`Y-`,x);

Nous voyons que Y+ se prolonge par continuité en zéro et donne même une fonction dérivable quel que soit le choix de la constante _C1. Par contre Y- n'admet une limite en zéro que pour une valeur particulière de _C1.

> `Y-0`:=subs(_C1=-2,`Y-`);

> series(`Y-0`,x);

Pour cette valeur particulière _C1=-2, nous obtenons une fonction dérivable à gauche de zéro. Pour que cette fonction dérivable se raccorde avec un Y+ il est nécessaire de spécifier la valeur de la constante _C1 dans Y+.

> `Y+0`:=subs(_C1=-1,`Y+`);

> series(`Y+0`,x);

Nous constatons que les fonctions Y-0 et Y+0 se raccordent en une fonction dérivable (et même de classe C^1) mais la fonction obtenue n'est pas deux fois dérivable en zéro. Cela ne l'empêche pas de fournir une solution, définie sur toute la droite réelle, pour l'équation différentielle proposée. C'est d'ailleurs la seule solution maximale définie au voisinage de zéro.

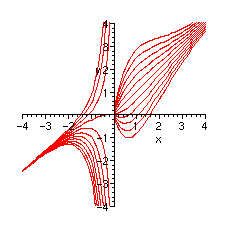
Le tracé des courbes intégrales illustre bien la situation.

> `picture-`:=plot({seq(subs(_C1=k,`Y-`),k=-5..5)},

                         x=-4..0,y=-4..4,color=red):

> `picture+`:=plot({seq(subs(_C1=k,`Y+`),k=-5..5)},

                          x=0..4,y=-4..4,color=red):

> plots[display]({`picture-`,`picture+`});

2. Passons à la seconde question. Notons qu'il ne s'agit pas d'une équation linéaire à cause de la valeur absolue qui porte sur le y. Notons aussi que la fonction nulle est évidemment solution. La discussion est plus subtile que dans le cas précédent parce qu'on ne peut pas préjuger du signe de la solution. Cependant nous avons envie de traiter deux équations comme dans le cas précédent et ces deux équations sont linéaires à coefficients constants d'ordre 2. Leur résolution est donc assurée. Simplement, il ne faut garder que les solutions positives ou négatives suivant le cas. Nous résolvons donc les équations linéaires et nous les tronquons grâce à la fonction d'Heaviside qui est la fonction caractéristique de l'ensemble des réels positifs.

> eq1:=diff(y(x),x,x)-2*y(x);

> Y1:=subs(dsolve(eq1,y(x)),Heaviside(y(x))*y(x));

> eq2:=diff(y(x),x,x)+8*y(x);

> Y2:=subs(dsolve(eq2,y(x)),Heaviside(-y(x))*y(x));

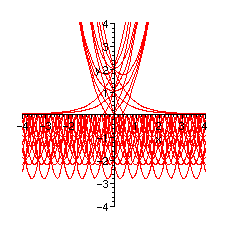
> picture1:=plot({seq(seq(subs(_C1=k,_C2=l,Y1),l=-2..2),k=-2..2)},

                         x=-4..4,y=-4..4,color=red):

> picture2:=plot({seq(seq(subs(_C1=k,_C2=l,Y2),l=-2..2),k=-2..2)},

                         x=-4..4,y=-4..4,color=red):

> plots[display]({picture1,picture2});

La question à traiter est maintenant plus claire (dans notre esprit, car elle est en elle-même sans aucune ambiguïté). Il faut dans chaque cas étudier les intervalles maximaux où les solutions des deux équations linéaires ont un signe constant. Ensuite il faut regarder s'il est possible de raccorder ces solutions à signe constant.

Première équation. Commençons par la première équation. La solution générique s'écrit

Si les deux constantes et sont nulles, nous avons affaire à la solution nulle. Écartons ce cas. Si la solution ne s'annule pas et a le signe de . Dans le cas elle s'écrit

et est définie partout. Dans le cas contraire elle est définie nulle part.

Ensuite si la solution s'annule aux racines de l'équation

Comme la tangente hyperbolique est strictement croissante et varie de -1 à 1, la discussion est facile. Si la solution ne s'annule pas et a le signe de (comme on le voit en regardant à l'infini). Donc si on a une solution sur toute la droite réelle et sinon pas de solution.

Enfin si , l'équation qui donne les points où s'annule la solution possède exactement une racine caractérisée par l'équation

En écrivant la solution sous la forme

nous voyons que si nous obtenons une solution définie pour   par contre dans le cas nous obtenons une solution définie pour .

Deuxième équation. Considérons maintenant les solutions de la deuxième équation. Elles s'écrivent

Bien sûr, nous retrouvons la solution nulle que nous écartons. En définissant un nombre strictement positif par

nous pouvons récrire les solutions sous la forme

Évidemment une telle fonction s'annule une infinité de fois. Les intervalles utiles sont ceux où elle est négative. Ils ont pour extrémités les et avec entier relatif.

Raccord. Maintenant la question qui se pose est de savoir s'il est possible de raccorder les solutions du premier type avec les solutions du second type pour franchir l'axe des abscisses. Nous calculons la dérivée d'une fonction du premier type et nous tenons compte de l'égalité

et de l'équation satisfaite par pour obtenir la valeur de la dérivée au point où le graphe de la fonction rencontre l'axe des abscisses. Cela nous donne la valeur

En choisissant les deux constantes, nous obtenons n'importe quel nombre réel non nul, positif ou négatif suivant le signe de .

De la même façon les fonctions du deuxième type ont comme dérivées aux points où elles s'annulent respectivement et . En choisissant le nombre on obtient n'importe quel nombre réel non nul.

Solutions maximales. Finalement on peut énumérer les solutions maximales de l'équation différentielle proposée. On remarquera d'ailleurs que cette équation satisfait les hypothèses du théorème de Cauchy-Lipschitz dans tout le plan des (x,y). Les solutions maximales sont de trois types. Il y a d'abord la solution nulle, définie sur toute la droite réelle. Ensuite il y a les solutions du premier type qui ne prennent que des valeurs strictement positives sur toute la droite réelle (cas , et , , ). Enfin il y a les solutions définies par morceaux. Précisément il y trois morceaux : de -infinity à un certain x0- on a une solution de la première équation ; on passe ensuite a une solution de la seconde équation en raccordant les dérivées ; ensuite en x0+=x0-+Pi*sqrt(2)/4 on raccorde avec une solution de la première équation.

Le dernier type de solution maximale est évidemment le plus compliqué. Pour étayer nos dires nous procédons à une petite expérience en construisons une solution de ce type. Nous choisissons arbitrairement une solution positive définie sur un intervalle de la forme ]-infinity,x0[.

> y1:=cosh(sqrt(2)*x)-2*sinh(sqrt(2)*x);

Nous déterminons le point où elle s'annule.

> `x0-`:=solve(y1,x);

Ensuite nous cherchons l'entier relatif à employer pour raccorder avec une solution de la seconde équation.

> evalf(`x0-`/(2*Pi/sqrt(2)));

Le calcul nous dit qu'il faut prendre . Nous définissons donc le deuxième morceau de la solution, en laissant le paramètre qui va permettre d'ajuster les dérivées.

> y2:=A*sin(2*sqrt(2)*(x-`x0-`)-Pi);

Nous comparons les comportements en x0- pour choisir le bon paramètre.

> series(y1,x=`x0-`,3);

> series(y2,x=`x0-`,3);

> y2:=subs(A=sqrt(3)/2,y2);

Ayant trouvé le deuxième morceau, nous allons voir ce qui se passe au point où il va revenir à zéro.

> `x0+`:=`x0-`+Pi/2/sqrt(2);

> series(y2,x=`x0+`);

Nous introduisons alors le troisième morceau en employant une solution de la première équation.

> y3:=K1*cosh(sqrt(2)*x)+K2*sinh(sqrt(2)*x);

Nous écrivons les équations qui expriment que le troisième morceau s'annule en x0+ et y possède la bonne dérivée.

> eq0:=subs(x=`x0+`,y3);

> eq1:=subs(x=`x0+`,diff(y3,x))=sqrt(3)*sqrt(2);

Nous déterminons ainsi les deux paramètres et nous substituons leurs valeurs.

> solve({eq0,eq1},{K1,K2});

> y3:=combine(convert(subs(%,y3),exp),exp);

La solution maximale est déterminée. Nous pouvons la tracer.

> plot(piecewise(x<=`x0-`,y1,x<=`x0+`,y2,y3),

                         x=`x0-`-2..`x0+`+2,color=red);

Retour en page principale