Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

La fonction génératrice correspondant à un lancer de dés est évidente.

> f1:=add(z^i,i=1..6)/6;

La somme des points obtenus en n lancers est une variable aléatoire qui est la somme de n variables aléatoires indépendantes et équidistribuées. La fonction génératrice de la somme est donc la puissance n-ième de la fonction génératrice associée à un lancer. Pour obtenir la probabilité que la somme ait une certaine valeur il suffit d'expliciter la fonction génératrice. Nous le faisons d'abord pour n=10.

> nb:=10:

> f.nb:=collect(f1^nb,z);

> for k from 0 to 6*nb do

    p[k]:=coeff(f10,z,k)

  od:

Nous disposons ainsi des probabilités et nous pouvons tracer le graphique demandé.

> plot([seq([k,p[k]],k=0..6*nb)]);

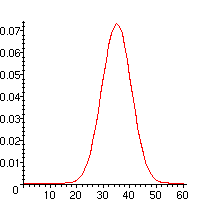
Recommençons avec n égal à 100. Le calcul devient laborieux parce qu'il faut développer un polynôme de degré 600 à coefficients rationnels. Il serait plus efficace de calculer (z+...+z^6)^100 et de diviser le tout par 6^100.

> nb:=100:

> st:=time():

  f.nb:=collect(f1^nb,z):

  time()-st;

> for k from 0 to 6*nb do

    p[k]:=coeff(f.nb,z,k)

  od:

> plot([seq([k,p[k]],k=0..6*nb)]);

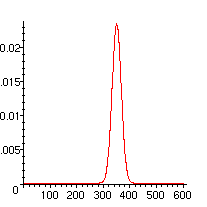
Nous obtenons une courbe similaire à la précédente, mais la probabilité est plus concentrée vers le centre de l'intervalle des valeurs (la somme prend ses valeurs entre n et 6n, ici entre 100 et 600).

Soyons plus précis. Nous employons la fonction génératrice, d'abord pour calculer la moyenne puis la variance et l'écart type de la somme.

> mu:=subs(z=1,diff(f.nb,z));

> subs(z=1,diff(f.nb,z,z)+diff(f.nb,z)-diff(f.nb,z)^2);

> sigma:=evalf(%^(1/2));

Ensuite nous regardons comment évoluent les probabilités quand la valeur k s'éloignent de l'indice qui donne le maximum.

> for xx from 0 to 5 do

    k:=round(mu+xx*sigma);

    print(k=evalf(p[k]))

  od:

Nous voyons qu'à partir de trois écarts type, la probabilité est négligeable.

Curieusement l'exercice demande une illustration, mais ne demande pas de tirer la moindre conclusion de cette expérience. Comme nous l'avons déjà indiqué, la variable aléatoire étudiée est la somme de n variables indépendantes équidistribuées. De plus la loi commune à ces variables possède une moyenne et une variance. Il en résulte que le théorème central limite s'applique et la fonction de répartition de la somme, convenablement normalisée, converge vers la loi normale. Nous allons mettre ceci en valeur.

D'abord nous calculons la moyenne et la variance de la distribution correspondant à un lancer.

> subs(z=1,diff(f1,z));

> subs(z=1,diff(f1,z,z)+diff(f1,z)-diff(f1,z)^2);

Ensuite nous allons graphiquement tester la convergence. Nous prenons une valeur de n qui est faible, faute de quoi il n'y aurait rien à voir tant la convergence est rapide.

> nb:=10:

> f.nb:=collect(f1^nb,z):

> for k from 0 to 6*nb do

    p[k]:=coeff(f10,z,k)

  od:

> mu:=nb*7/2;

> sigma2:=nb*35/12;

Nous traçons comme plus haut la distribution discrète, puis nous traçons la gaussienne convenablement calée. Nous aurions aussi pu normaliser la distribution discrète. Nous aurions aussi pu employer les fonctions de répartition, pour coller à l'énoncé du théorème central limite.

> exact:=plot([seq([k,p[k]],k=0..6*nb)],color=red):

> approx:=plot(1/sqrt(2*Pi*sigma2)*exp(-(x-mu)^2/2/sigma2),

                                     x=0..6*nb,color=blue):

> plots[display]({exact,approx});

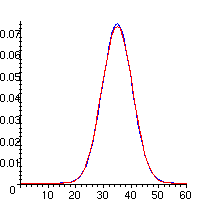
L'accord est si bon que nous avons du mal à distinguer les deux courbes.

Sur le théorème limite central, on peut par exemple consulter [Renyi66].

Retour en page principale