Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet Maple V.5 worksheet

Illustration | Principe d'André | Série génératrice

Illustration. Il est naturel d'employer comme espace probabilisé l'ensemble des parties à quarante éléments de l'ensemble des entiers entre 1 et 100. Autrement dit les clients portent chacun un numéro entre 1 et 100 et on distingue les quarante qui n'ont que des billets de 100FF. Nous munissons cet espace de l'équiprobabilité. Notons au passage que l'effectif est un simple binomial.

> binomial(100,40);

Si nous voulons réaliser une petite expérience, nous effectuons un tirage au hasard d'une partie à quarante éléments de l'ensemble des entiers entre 1 à 100. Le logiciel nous fournit deux outils pour cela. Le premier est une procédure du package combinat.

> S:=combinat[randcomb](100,40);

Le second est une procédure du package combstruct.

> S:=combstruct[draw](Combination(100),size=40);

Le package combstruct est un outil extrêmement puissant tourné vers l'étude de structures combinatoires, dans l'esprit actuel de la combinatoire influencé par la théorie des langages formels et des structures de données informatiques. Je ne peux que vous encourager à lire les pages consacrées à combstruct.

Muni de ce tirage aléatoire d'ensemble, nous pouvons illustrer la situation. Un client muni d'un billet de 50FF fournit ce billet au caissier et le nombre de billets de 50FF dont dispose celui-ci augmente d'une unité. A contrario un client muni d'un billet de 100FF oblige le caissier à lui rendre un billet de 50FF et le nombre de billets de 50FF dont dispose celui-ci diminue d'une unité. Représentons alors le le nombre de billets de 50FF dont dispose le caissier au cours du temps. Nous obtenons un chemin dans le plan Z^2, qui part de l'origine (0,0) et qui va au point (100,20). Ce chemin comporte cent pas et chaque pas est un déplacement de (1,1) ou de (1,-1). Illustrons ceci.

> T:='T':

  for s in S do T[s]:=1 od:

  w[0]:=0:

  for i to 100 do

    if assigned(T[i]) 

    then w[i]:=w[i-1]-1

    else w[i]:=w[i-1]+1

    fi

  od:

> plot([seq([i,w[i]],i=0..100)],color=red);

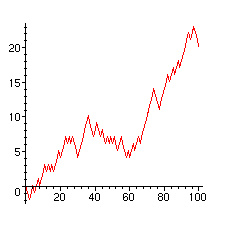
Le problème revient à compter les chemins qui restent au dessus de l'axe des abscisses. En fait nous allons compter l'ensemble complémentaire.

Principe d'André. Pour évaluer le nombre de chemin qui passe strictement sous l'axe des abscisses, nous employons le principe de réflexion de Désiré André [Comtet70, tome 1, page 33]. Pour l'expliquer, contentons nous d'un chemin à dix pas dont quatre vers le bas. En voici un exemple.

> S:={2,4,5,8};

> T:='T':

  for s in S do T[s]:=1 od:

  w[0]:=0:

  for i to 10 do

    if assigned(T[i]) 

    then w[i]:=w[i-1]-1

    else w[i]:=w[i-1]+1

    fi

  od:

> graph[1]:=plot([seq([i,w[i]],i=0..10)],color=red):

> graph[1];

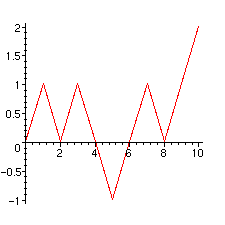
Nous considérons le dernier instant où le chemin est sous l'axe des abscisses au sens strict et nous retournons la partie qui précède, comme suit.

> for i from 10 to 0 by -1 while w[i]>=0 do

    ww[i]:=w[i]

  od:

  for j from i to 0 by -1 do

    ww[j]:=-2-w[j]

  od:

> graph[2]:=plot([seq([i,ww[i]],i=0..10)],color=blue):

> graph[2];

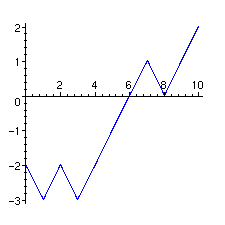
Le dessin suivant met bien en valeur la réflexion.

> plots[display]({graph[1],graph[2]});

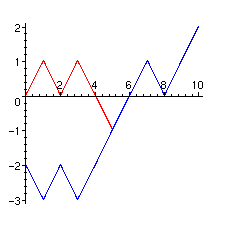
Cette rélexion transforme un chemin qui va de (0,0) à (100,20) et qui passe strictement sous l'axe des abscisses en un chemin qui va de (0,-2) à (100,20) et la correspondance est bijective. Le nombre de tels chemins est égal au binomial binomial(100,39). En effet si x est le nombre de montées et y le nombre de descentes, on a d'une part x+y=100 et d'autre part x-y=22.

Nous pouvons évaluer le nombre des chemins qui ne conviennent pas et la probabilité demandée.

> binomial(100,39);

> 1-binomial(100,39)/binomial(100,40);

Plus généralement, si le chemin comporte N pas dont n vers le bas, on obtient le résultat suivant.

> p:=1-binomial(N,n-1)/binomial(N,n);

> simplify(convert(p,GAMMA));

Série génératrice. La méthode précédente a le mérite d'être élémentaire. Nous allons maintenant employer une méthode plus sophistiquée et dont le champ d'application est beaucoup plus vaste que le principe de réflexion.

Nous notons f[n,k] le nombre de chemin en n pas partant de (0,0), arrivant à la hauteur k, c'est-à-dire en (n,k), et qui reste au dessus de l'axe des abscisses. Dans l'exemple que nous traitons f[n,k] est nul dès que n et k n'ont pas la même parité. Cependant cette remarque n'est plus nécessairement valable si l'on change l'ensemble de pas autorisés. Ensuite nous définissons la suite des polynômes

----- \ k f[n](u) = ) f[n, k] u / ----- k

qui codent les marches en n pas. Dans l'exemple, l'indice k de la somme précédente varie entre -n et n.

Oublions un instant la restriction qui impose un chemin au dessus de l'axe des abscisses. Alors le lien entre f[n](u) et f[n+1](u) est simplement traduit par la formule

f[n + 1](u) = P(u) f[n](u),

avec la condition initiale f[0](u)=1, qui exprime qu'il n'y a qu'un chemin en zéro pas de (0,0) à (0,0). On peut aisément tester cette récurrence.

> P:=u+1/u;

> f:=1;

  for i to 5 do

    f:=collect(P*f,u)

  od;

On voit bien apparaître les coefficients binomiaux attendus.

Si maintenant on interdit que le chemin passe sous l'axe des abscisses, il faut corriger la formule de récurrence. On doit enlever à chaque étape les chemins qui passent sous l'axe des abscisses au dernier pas. Dans l'exemple simple que nous traitons, le pas négatif de hauteur -1 ne peut amener le chemin à devenir négatif que si la hauteur à l'étape précédente était 0. Or le nombre de chemin en n pas qui termine à la hauteur 0 est le coefficient constant de f[n], c'est-à-dire f[n](0). On obtient donc la formule

f[n](0) f[n + 1](u) = P(u) f[n](u) - -------. u

Si les pas négatifs étaient autres, le terme correctif comprendrait des dérivées de f[n] évaluées en 0. Nous pouvons tester cette récurrence pour de faibles valeurs.

> f:=1;

  for i to 5 do

    f:=collect(P*f-1/u*subs(u=0,f),u)

  od;

Nous pourrions aisément vérifier que les valeurs obtenues sont correctes. Avec ce schéma de calcul, nous pouvons à nouveau traiter la question posée.

> f:=1:

  for i to 100 do

    f:=collect(P*f-1/u*subs(u=0,f),u)

  od:

  coeff(f,u,20)/binomial(100,40);

Bien sûr, nous obtenons le même résultat.

Considérons maintenant la série génératrice double

----- \ n k F(z, u) = ) f[n, k] z u / ----- n,k>=0

c'est-à-dire

----- \ n F(z, u) = ) f[n](u) z / ----- n

avec les notations précédentes. La relation de récurrence sur les f[n](u) se traduit en l'équation

/----- \ /----- \ | \ n| | \ n| F(z, u) = f[0](u) + z P(u) | ) f[n](u) z | - z/u | ) f[n](0) z |, | / | | / | |----- | |----- | \ n / \ n /

soit encore

1 - z/u F(z, 0) F(z, u) = ---------------. 1 - z P(u)

On notera que la présence du terme 1/u F(z,0) vient du fait que le pas négatif a pour hauteur -1. S'il y avait eu un pas négatif de hauteur -2, on aurait vu apparaître un terme produit de 1/u^2 par la dérivée parteille de F par rapport à u évaluée en (z,0).

Appelons right_hand_side le membre droit de la dernière équation. Il s'évalue comme suit.

> P:=u+1/u;

> right_hand_side:=normal((1-F0/u)/(1-z*P));

Le dénominateur est du second degré en u, ce qui fait que dans cet exemple nous pouvons explicitement évaluer ses racines.

> branch_list:=[solve(denom(right_hand_side),u)];

Une application de la procédure series nous montre que pour z proche de 0, l'une des deux racines est proche de 0 alors que l'autre s'en va à l'infini.

> map(series,branch_list,z,3);

Or la série double qui définit F converge dès que l'on impose |u|<1 et |z|<1/2, parce que la somme des f[n,k] à n fixé ne peut sûrement pas excéder le nombre de marches sans contrainte en n pas, qui vaut 2^n. Il est donc possible de substituer la racine du dénominateur qui est proche de 0 dans la relation dénominateur * F(z,u)=numérateur. Ceci fournit une relation qui permet de calculer F(z,0) et donc F(z,u).

> U:=select(proc()

              evalb(op(2,series(args[1],z))>=0)

            end

            ,branch_list);

> eq:=subs(u=U[1],numer(right_hand_side));

> solve({eq},{F0});

> Fsol:=normal(subs(%,right_hand_side));

Ainsi F(z,0) et F(z,u) sont déterminés. Nous pouvons vérifier que le résultat est cohérent avec les calculs précédents.

> S:=series(Fsol,z,101):

> f100:=coeff(convert(S,polynom),z,100);

> coeff(collect(f100,u),u,20);

> coeff(f,u,20);

> collect(f100-f,u);

Le point remarquable est que la série double F(z,u) est algébrique. De plus le procédé employé, appelé méthode du noyau, est beaucoup plus souple que la méthode combinatoire que nous avons d'abord présentée. Il est possible de généraliser le problème de manière variée et sur ce sujet, on pourra consulter l'item Analytic Combinatorics and Random Walks dans la page de Cyril Banderier. Pour approfondir la question et assimiler la méthode du noyau, on pourra lire [Knuth68, sect. 2.2.1, ex. 4 et 11] et les deux contributions de Mireille Bousquet-Mélou (Sorted and/or sortable permutations) et Marko Petkovsek (The irrational chess knight) à [FPSAC'98].

Retour en page principale