Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale Table des matières Index

Maple V.4 worksheet, bis, ter, quatro Maple V.5 worksheet, bis, ter, quatro

1 | 2 | 2 bis | 3

1. On pourrait suivre la même voie que pour l'exemple 31 de la page 251, en démarrant de la manière suivante. On obtient d'ailleurs la même relation de récurrence ; seules les valeurs initiales diffèrent.

> student[intparts](Int(arccos(x)^n,x),arccos(x)^n);

> simplify(%,power);

Nous allons suivre une autre voie, fondée sur l'expérimentation. Nous commençons par calculer les premières valeurs de la suite d'intégrales.

> for nn to 3 do 

    student[changevar](arccos(x)=t,

                       Int(arccos(x)^nn,x),t)

  od;

Le système a besoin d'être poussé dans le bon sens. N'hésitons pas.

> for nn to 3 do 

    subs(sqrt(1-cos(t)^2)=sin(t),

         student[changevar](arccos(x)=t,

                            Int(arccos(x)^nn,x),t))

  od;

> for nn to 5 do 

    value(subs(sqrt(1-cos(t)^2)=sin(t),

               student[changevar](arccos(x)=t,

                                  Int(arccos(x)^nn,x),t)))

  od;

Pour revenir à la question, il suffit de remplacer respectivement t par Arccos(x), cos(t) par x et sin(t) par sqrt(1-t^2).

Nous regardons les résultats obtenus et nous voyons que l'intégrale d'indice n a pour terme de tête t^n*cos(t). Le reste de l'expression s'obtient en multipliant le résultat précédent par n avec un échange simple sur le sinus et le cosinus. Nous testons une procédure qui mime la récurrence que nous voyons.

> f:=proc(n::nonnegint)

    option remember;

    t^n*cos(t)

     +n*subs({cos(t)=-sin(t),sin(t)=cos(t)},f(n-1))

  end:

  f(0):=cos(t):

> for nn to 5 do nn,f(nn) od;

Il semble que nous obtenions ainsi les bonnes valeurs. Regardons mieux les valeurs obtenues. En divisant par la factorielle, on voit les troncatures des series de cos(t) et sin(t). Par exemple, dans le dernier résultat qui correspond à n=5, si l'on divise le coefficient de cos(t) par n!=120, on voit t-t^3/6+t^5/120, qui est la troncature de rang 5 de la série du sinus. Or si nous avons une série génératrice F(z)=sum(fk*t^k,k=0..infinity), la série génératrice des troncatures sum(fk*t^k,k=0..K) vaut F(t*z)/(1-z), comme on peut s'en convaincre par l'instruction suivante.

> series(F(t*z)/(1-z),z);

Pour le cas qui nous occupe, nous avons pour l'intégrale d'indice n quelque chose comme cos(t)*sin_n(t)+sin(t)*cos_n(t), en notant d'un indice l'ordre de la troncature. Ceci nous fait considérer l'expression suivante.

> series(cos((1-z)*t)/(1-z),z);

Nous voyons que nous ne sommes pas loin de ce qu'il faut mais ce n'est pas exactement cela. Une réflexion plus approfondie nous amène à l'expression suivante. Pour l'obtenir nous avons utilisé le fait que la partie paire d'une série génératrice f(z) est (f(z)+f(-z))/2 et la partie impaire vaut (f(z)-f(-z))/2. De plus pour faire apparaître un (-1)^k dans une série paire en z^(2*k), il suffit de changer z en I*z. Bref, nous prétendons que l'expression suivante est celle qui convient. Elle fournit la série génératrice de la suite d'intégrales (exprimées en fonction de t, mais ceci ne pose pas problème).

> result:=cos(t)*subs(F=cos,

                   1/2/(1+I*z)*F(-I*t*z)+1/2/(1-I*z)*F(I*t*z))

    +sin(t)*subs(F=sin,

                   1/2/(1+I*z)*F(-I*t*z)+1/2/(1-I*z)*F(I*t*z))

    +cos(t)*subs(F=sin,

                   -I/2/(1-I*z)*F(I*t*z)+I/2/(1+I*z)*F(-I*t*z))

    -sin(t)*subs(F=cos,

                   -I/2/(1-I*z)*F(I*t*z)+I/2/(1+I*z)*F(-I*t*z));

Vérifions que le calcul n'est pas grossièrement faux.

> map(expand,series(result-add(f(i)*z^i/i!,i=0..16),z,16));

Il suffit maintenant de rendre le résultat plus lisible.

> collect(result,[sin(t),cos(t)],normal@evalc);

> sol:=normal(subs(cosh(t*z)+sinh(t*z)=exp(t*z),%));

Il suffirait maintenant d'exprimer le terme général de cette série génératrice par un produit de Cauchy et de prouver que l'expression est bien correcte.

Retour en haut de page

2. Dans cet exemple, nous allons prendre le problème à l'envers. Au lieu que nous trouvions une méthode de calcul et que nous l'appliquions en Maple, nous allons regarder comment le calcul de ces intégrales est réalisé dans le logiciel.

Tout d'abord nous constatons que le système de calcul nous renvoie une réponse.

> int((sin(x)/x)^4,x=0..infinity);

Cependant si nous augmentons la valeur du paramètre entier, un problème surgit.

> int((sin(x)/x)^15,x=0..infinity);

Cette limite non évaluée nous indique que le calcul de l'intégrale passe d'abord par un calcul de primitive. On prend ensuite les limites aux bornes. Ici le calcul de limite échoue parce que les développements asymptotiques utilisés ne sont pas assez précis. Il suffit d'augmenter la précision pour obtenir le résultat, en modifiant la valeur de la variable Order. Cependant, inconvénient des tables de remember, si l'on se contente de modifier la valeur d'Order, on obtient le même résultat car il n'y pas une nouvelle évaluation de l'intégrale mais lecture dans une table de remember. Pour que le calcul soit effectué et tienne compte de la nouvelle valeur d'Order,, il faut vider la table de remember. Mais on ne sait pas où est exactement cette table. En fait la procédure int n'a pas l'option remember et c'est la procédure auxiliaire int/int dont il faut vider la table par l'instruction (ceci est valable en Maple V.5). Il suffit pour cela d'employer la procédure forget comme suit (ceci est valable dans toutes les versions).

> readlib(forget):

> forget(int);

On peut aussi être beaucoup plus brutal et employer un restart, mais cela remet tout le système dans son état initial.

> restart:

> Order:=40:

> int((sin(x)/x)^15,x=0..infinity);

On obtient ainsi le bon résultat.

Puisque le calcul des intégrales passe par le calcul de primitives, nous allons nous contenter de calculer des primitives. Pour comprendre la méthode employée, nous augmentons le niveau d'affichage des calculs jusqu'à 100. Ceci va provoquer une avalanche de texte. Pour éviter cette conséquence désagréable, nous dirigeons l'écriture vers un fichier output.txt. Nous effectuons le calcul puis nous redirigeons l'écriture vers la sortie standard.

> restart:

> writeto(`output.txt`):

> printlevel:=100:

> int((sin(x)/x)^5,x);

> printlevel:=1:

> writeto(terminal):

Nous avons ainsi créé le fichier output.txt, qui est assez long (de l'ordre de 100K). Nous allons le commenter et il sera plus agréable de le lire dans une nouvelle fenêtre. Si cela vous gêne vous pouvez aussi le lire dans cette fenêtre. Pour faciliter la lecture nous l'avons truffé de marque de la forme #xx (et mis en mode html).

On démarre (#01) en appelant int, qui appelle tout de suite (#02) sa procédure auxiliaire int/int. Rappelons que nous travaillons en Maple V.5 et les appels de procédure ne se dérouleraient pas de la même façon en V.3 ou en V.4. La syntaxe est vérifiée (#03). Une normalisation des noms de variables s'effectue (#04) ; elle n'a pas d'effet visible. Enfin (#05) on entre dans le vif du sujet en appelant la procédure d'intégration indéfinie int/indefinite, qui appelle elle-même int/indef0 et int/indef1. On peut voir le code de cette procédure int/indef1 par les instructions (print fait tout aussi bien l'affaire que readlib si l'on a déjà employé la procédure)

> interface(verboseproc=2):

  readlib(`int/indef1`);

La procédure int/indef1 (#06) regarde dans la table int/itable si la primitive est connue, mais ce n'est pas le cas (#07). Du coup on analysel'expression (#08). Comme on voit que c'est un produit, on met de côté un éventuel coefficient indépendant de la variable mais ici il vaut 1 (#09). On vérifie que l'expression à primitiver ne comporte pas de radical (#10) et on entre dans la procédure int/indef2 (#11). On peut voir le code de cette procédure par l'instruction

> readlib(`int/indef2`);

(on a déjà rendu les procédures verbeuses à la ligne précédente)

On démonte un peu l'expression (#12). On regarde si l'expression à primitiver n'est pas de la forme F(u)*u' (#13). Cela échoue et on appelle int/trigon à cause de la présence du sinus (#14). La forme de l'intégrande fait appeler int/xsincos (#15) et ceci provoque une linéarisation par tfourier/sin (#16). On se retrouve avec une somme en sin(5*x)/x^5, sin(3*x)/x^5 et sin(x)/x^5 (#17). On redémarre sur l'intégration de cette somme, ce qui fait entrer dans int/indef1, puis encore int/indef1 pour traiter chaque terme de la somme (#18). Après avoir enlevé le coefficient qui est en facteur, on doit intégrer sin(5*x)/x^5 (#19) et pour cela on passe dans int/indef2 (#20). On procède au changement de variables x=5*x (#21) et pour intégrer 625*sin(x)/x^5 on entre a nouveau dans int/indef1 (#22). Le coefficient 625 est mis de côté, d'où une nouvelle entrée dans int/indef1 (#23). Là c'est int/xsincos qui fournit le résultat, en employant des formules de récurence fondées sur l'intégration par parties (#24). On peut le voir en lisant le code d'int/xsincos par l'instruction

> readlib(`int/xsincos`);

Pour intégrer x^m*sin(x)^n*cos(x)^p, int/xsincos prend en entrée le triplet m,n,p.

On traite ensuite le terme en sin(3*x)/x^5 (#25), puis le terme en sin(x)/x^5 (#26) par la même méthode. Les résultats précédents se sont accumilés dans les tables de remember et cela ne donne pas lieu à de nouveaux calculs. On ressort donc de int/trigon avec ces résultats qui sont assemblés (#27). On dépile tous les appels pour ressortir finalement d'int (#28).

Finalement le calcul de l'intégrale proposée en exercice se déroule comme suit : il y a linéarisation de la puissance du sinus, changement de variables linéaire dans les sin(k*x) obtenus, puis intégration par parties sur les sin(x)/x^n. Ensuite il faut évaluer les valeurs de la primitive aux bornes de l'intervalle ; cela demande des développements limités en 0 avec une précision au moins en x^n et c'est pourquoi la variable Order intervient dans le calcul.

Retour en haut de page

2 bis. Il faut bien dire que jusqu'ici nous n'avons pas répondu à la question : nous n'avons pas indiqué de récurrence ou de formule générale pour l'intégrale proposée. Nous cherchons donc une formule de récurrence en employant l'intégration par parties. Mais pour cela nous généralisons le problème en permettant que les exposants du sinus et de la variable soient différents. Autrement dit nous considérons l'intégrale

.

Cette intégrale est convergente si k et n sont supérieurs ou égaux à 2 avec k inférieur ou égal à n ou si k égale 1 et n est impair.

Pour obtenir une formule de récurrence, nous travaillons avec les primitives et non avec les intégrales de manière à éviter l'évaluation aux bornes.

> expr[0]:=Int(sin(x)^(n+2)/x^(k+2),x);

> student[intparts](expr[0],sin(x)^(n+2));

> map(readlib(`combine/trig`),%);

> expr[1]:=combine(subs(exp(k*ln(x)+2*ln(x))=x^(k+2),%),power);

> student[intparts](expr[1],sin(x)^(n+1)*cos(x));

> map(expand,%);

> subs(cos(x)^2=1-sin(x)^2,%);

> map(expand,%);

> expr[2]:=map(combine,%,power);

Nous voyons que nous avons obtenu la récurrence cherchée. Nous la mettons en valeur en effectuant la différence entre l'expression de départ et l'expression que nous venons d'obtenir. De plus nous sommes intéressés par les intégrales et non par les primitives. Nous évacuons donc les termes qui ne comportent pas le signe d'intégration. Ils ont pour limite zéro en zéro et à l'infini, dans la mesure où nous astreignons n et k à être dans l'ensemble que nous avons indiqué plus haut (2 <= k <= n ou k=1 et n impair).

> Rec:=expr[0]-select(has,expr[2],{int,Int});

Pour insister, nous mettons en valeur les intégrales qui demeurent.

> Indets:=select(has,indets(Rec),{int,Int});

Nous explicitons la récurrence obtenue. Plutôt que de bricoler l'expression ci-dessus, nous écrivons une petite procédure qui donne l'exposant d'un pseudo-monôme expr par rapport à une expression x. Nous allons voir à l'usage ce qu'il faut entendre par pseudo-monôme.

> toto:=proc(expr,x)

  local i;

  if not has(expr,x) then RETURN(0) fi;

  if expr=x then RETURN(1) fi;

  if type(expr,`*`) then

    RETURN(add(toto(i,x),i=expr))

  fi;

  if type(expr,`^`) then

      RETURN(toto(op(1,expr),x)*op(2,expr))

  fi;

  0

end:

Nous testons cette procédure sur un exemple.

> toto(1/(sin(x)^n/(x^m*sin(x)^p)/x^r),sin(x));

Cet outil nous permet d'obtenir facilement la récurrence.

> for i in Indets do

  op1:=op(1,i);

  tosubs[i]:=u(toto(op1,sin(x)),-toto(op1,x))  

od:

> rec:=subs(seq(i=tosubs[i],i=Indets),Rec);

> rec:=collect(numer(rec),u,factor);

Le résultat obtenu montre qu'il y a deux cas à considérer. Celui où n et k ont la même parité et celui où ils sont de parités contraires. Pour rendre ceci plus clair, nous produisons un petit dessin.

> threecolors:=proc(n,k)

  if type(n,posint) and type(k,posint) then

    if k>n then black

    elif k=1 and type(n,even) then black

    elif type(n-k,even) then red

    else blue

    fi

  else

    'threecolors'(n,k)

  fi  

end:

> N:=10:

> for nn to N do for kk to N do

  SQ:=[[kk,-nn],[kk,-nn-1],[kk+1,-nn-1],[kk+1,-nn]];

   pic[nn,kk]:=plots[polygonplot](SQ,

            color=threecolors(nn,kk),

            view=[-2..N+1,-N-1..2]);

od od:

> pic[text]:=plots[textplot]([seq([0,-n-1/2,convert(n,string)],

                                                          n=1..N),

      seq([k+1/2,0,convert(k,string)],k=1..N)],

                          font=[TIMES,ROMAN,10]):

> plots[display]({seq(seq(pic[n,k],k=1..N),n=1..N),pic[text]},

                                   scaling=constrained,axes=none);

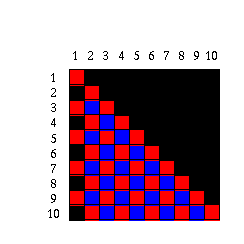
Les lignes sont indexées par n et les colonnes sont indexées par k. Pour un couple qui donne une intégrale divergente, la case associéee est noire. Les couples (n,k) pour lesquels n et k ont la même parité sont en rouge et ceux pour lesquels n et k sont de parités contraires sont en bleu. La récurrence fait que l'on dispose de J(n+2,k+2) si l'on connaît J(n+2,k) et J(n,k). Le remplissage des cases rouges et le remplissage des cases bleues sont donc complétement indépendants. Pour remplir les cases bleues il faut connaître le contenu de celles qui sont dans la colonne k=2 et dans la colonne k=3. Pour remplir les cases rouges, il faut connaître le contenu de celles qui sont dans la colonne k=1 et dans la colonne k=2.

Cas k=1, n impair. Commençons par nous intéresser aux cases rouges de la première colonne. Bien que pourvu d'un puissant système de calcul, nous sommes encore capables de travailler à l'ancienne. Une bonne vieille linéarisation par les formules d'Euler et la connaissance du cas de base

ou plutôt de l'intégrale de Dirichlet (a>0)

nous amène à la formule

.

Les esprits inquiets peuvent d'ailleurs tester cette formule comme suit.

> for pp from 0 to 10 do nn:=2*pp+1;

    print(nn,

          int(sin(x)^nn/x,x=0..infinity),

          Pi/2*add((-1)^qq*binomial(nn,pp-qq),qq=0..pp)/2^(2*pp))

  od:

Cependant la somme s'évalue.

> sum((-1)^q*binomial(2*p+1,p-q),q=0..p);

Nous avons donc obtenu la formule

c'est-à-dire

On voit alors aisément que les termes de la première colonne satisfont la récurrence (p>0)

,

mais je ne vois pas comment obtenir cette formule directement.

Cas k=2, n pair. Passons aux cases rouges de la deuxième colonne. L'entier n est donc pair au moins égal à 2 et k vaut 2. À nouveau nous employons la linéarisation. Ceci fait apparaître des cosinus et l'on peut avoir un instant de doute pour ce qui est de la convergence des intégrales. Cependant la somme des coefficients qui apparaissent dans la formule est nulle. On le voit par exemple en considérant le comportement en zéro de la somme obtenue et du sinus à la puissance n. On peut d'ailleurs tester cette nullité avec le système.

> sum((-1)^q*binomial(2*p,q),q=0..p-1)+(-1)^p/2*binomial(2*p,p);

Du coup nous récrivons la somme en soustrayant 1 à chaque cosinus et ceci nous ramène aux intégrales que voici.

> student[changevar](a*x=z,Int((cos(a*x)-1)/x^2,x=0..infinity));

Il suffit donc de connaître celle-ci, qui s'obtient d'ailleurs en opérant une intégration par parties sur l'intégrale de Dirichlet.

> int((cos(x)-1)/x^2,x=0..infinity);

On en tire d'abord le résultat suivant

.

Mais le système nous fournit la somme et nous arrivons à la formule (p>0)

.

Comme dans le cas précédent, le calcul que voici

> expr:=Pi*(p+1)*binomial(2*p,p-1)/(2^(2*p)*(2*p-1));

> simplify(convert(subs(p=p+1,expr)/expr,GAMMA),GAMMA);

nous fournit une récurrence verticale (la verticalité fait référence au tableau dessiné plus haut)

.

Cas k=2, n impair. Il faut maintenant traiter les cases bleues de la deuxième colonne (n impair au moins égal à 3, k=2). Un test montre tout de suite une différence qualitative avec les deux cas précédents.

> for pp from 1 to 10 do nn:=2*pp+1;

    print(nn,int(sin(x)^nn/x^2,x=0..infinity))

  od:

Nous laissons au lecteur le plaisir de trouver par lui-même la formule générale, en employant les mêmes idées que précédemment. Les calculs suivants pourront peut-être l'inspirer.

> expr:=int(sin(a*x)/x^2,x);

> series(expr,x);

> asympt(expr,x);

Au bout du compte on arrive à la formule (p>0)

.

Ici le système ne nous fournit pas de formule sommatoire.

Cas k=3, n pair. Il reste à traiter les cases bleues de la troisième colonne (n pair au moins égal à 4, k=3). À nouveau, les calculs qui suivent devrait aider le lecteur à trouver la voie qui mène à la bonne formule.

> expr:=int((cos(a*x)-1)/x^3,x);

> series(expr,x);

> asympt(expr,x);

On arrive ainsi à la formule (p>1)

.

Procédure. Ayant couvert tous les cas de base nous pouvons écrire une procédure de calcul des intégrales J(n,k).

> Jproc:=proc(n::posint,k::posint)

    option remember;

    local p,q;

    if n<k then

      ERROR("the first argument should be not smaller

                                                 than the second")

    fi;

    p:=iquo(n,2);

    if k=1 then

      if type(n,odd) then

        Pi/2^n*(p+1)/n*binomial(n,p)

      else

        ERROR("the first argument should not be even,

                                             when the second is 1")

      fi

    elif k=2 then

      if type(n,odd) then

        -add((-1)^q*binomial(n,p-q)*(2*q+1)*ln(2*q+1),q=0..p)

                                                       /2^(2*p)

      else

        Pi/2^n*binomial(n,p-1)*(p+1)/(n-1)

      fi

    elif k=3 and type(n,even) then

      add((-1)^q*binomial(2*p,p-q)*q^2*ln(q),q=1..p)/2^(n-2)

    else

     (-n*Jproc(n,k-2)+(n-1)*Jproc(n-2,k-2))*n/(k-1)/(k-2)

     fi

  end:  

Pour comparer les valeurs renvoyées par Jproc avec celles fournies par int, le seul problème qui demeure est la non unicité de l'écriture des combinaisons linéaires de logarithmes d'entiers à coefficients des rationnels.

Pour terminer cette question, il faut signaler que la suite double des J(n,k) est liée à la suite des nombres eulériens. Le nombre eulérien compte le nombre de permutations des entiers de 1 à n à k montées [Comtet70, tome 2, chap. VI, sect. 5, p. 82]. Ces nombres satisfont la récurrence double

.

Surtout, Jean-Louis Nicolas [Nicolas92] a montré qu'ils admettent la représentation intégrale

On voit que dans le cas , on retrouve les intégrales que nous considérons ici. De plus dans le même article est citée la formule valable pour n pair et k entre 2 et n,

La preuve de cette formule repose sur le calcul de l'intégrale double

.

Retour en haut de page

3. Nous ne doutons pas que l'aimable lecteur ait obtenu une relation de récurrence en employant une intégration par parties.

> student[intparts](Int(ln(x)^n,x),ln(x)^n);

> map(combine,%,power,symbolic);

Nous préférons considérer la série génératrice exponentielle des ln(x)^n,

.

Pour que le calcul qui suit soit justifié, on peut considérer que la variable x se promène dans un segment [a,A] avec a et A strictement positifs et que la variable t est dans un segment [-r,r] avec r strictement positif. On primitive la série génératrice et cela donne la série génératrice exponentielle des primitives. À dire vrai ceci est incorrect, parce qu'il y a un choix de constantes à chaque primitive. Il faudrait spécifier comment est choisie la constante pour chaque primitive.

> gf:=int(exp(t*ln(x)),x);

Comparons les premiers coefficients de la série et les primitives fournies par le système.

> s0:=series(gf,t);

> s1:=add(int(ln(x)^nn,x)*t^nn/nn!,nn=0..5):

> series(s0-s1,t):

> map(collect,%,{x,ln(x)});

Il y a bien adéquation. On voit que pour ce qui est des constantes, on peut dire que les primitives ont pour limite 0 en 0.

La série génératrice exponentielle nous fournit une expression explicite de ces primitives. En effet elle s'écrit

et il suffit d'employer le produit de Cauchy pour obtenir la primitive d'indice n demandée dans l'exercice

.

Disposant de la série génératrice, on peut revenir vers la récurrence. Nous employons pour cela le package gfun de la bibliothèque partagée des utilisateurs.

> with(share):

  with(gfun):

See ?share and ?share,contents for information about the share library

Share Library:  gfun

Authors: Salvy, Bruno and Zimmermann, Paul.

Description:  package for the manipulation and discovery

  of generating functions

La procédure holexprtodiffeq du package gfun fait passer d'une expression holonome à une équation différentielle linéaire à coefficients polynomiaux satisfaite par l'expression.

> deq:=holexprtodiffeq(x*exp(t*ln(x))/(t+1),y(t));

La procédure diffeqtorec du package gfun fait passer d'une équation différentielle holonome à une récurrence holonome portant sur les coefficients du développement de Taylor des coefficients.

> rec:=diffeqtorec(deq,y(t),u(n));

Nous obtenons une récurrence linéaire d'ordre 2. On pourrait vérifier que la récurrence évoquée au début de la question implique celle-ci.

Retour en haut de page

Retour en page principale