Philippe.Dumas@inria.fr


http://algo.inria.fr/dumas/Maple/

Retour en page principale

Retour en page principale Table des matières Index

Maple V.4 worksheet, bis, ter Maple V.5 worksheet, bis, ter

1 | 2 | 3 | 4 | 5 | 6

L'article défini le employé dans l'énoncé est inapproprié. En effet un développement asymptotique dépend de l'échelle employée et de la précision que l'on fixe. Pour chacun des exemples, il s'avère qu'une échelle asymptotique se met naturellement en place et que l'on peut fournir des développements à une précision arbitraire dans cette échelle. La précision dépend de la variable Order. Nous nous contenterons généralement de la valeur par défaut, qui est 6.

1. Le premier exemple est assez particulier.

> F:=Int(ln(t)/t^2,t=x..infinity);

En effet une intégration par parties fournit un résultat explicite.

> student[intparts](F,ln(t));

> value(%);

Retour en haut de page

2. Considérons le deuxième exemple.

> F:=Int(exp(x*cos(t)),t=0..Pi/2);

Pour comprendre la situation, nous traçons le graphe de l'intégrande pour une valeur un peu élevée du paramètre.

> xx:=10:

> plot(exp(xx*cos(t)),t=0..Pi/2);

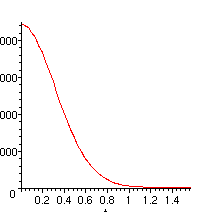
Le cosinus varie de 1 à 0 quand la variable va de 0 à Pi/2. Du coup les valeurs les plus grandes de la fonction sont atteintes au voisinage de 0 et c'est le comportement de la fonction au voisinage de 0 qui va dicter le comportement de l'intégrale. Pour mettre en valeur l'intervention du cosinus, nous procédons à un changement de variables.

> G:=student[changevar](cos(t)=1-u,F,u);

Nous mettons en facteur la valeur à la borne où est atteint le maximum, c'est-à-dire exp(x), et il nous reste à étudier l'intégrale suivante.

> H:=Int(exp(-x*u)/sqrt(2*u-u^2),u=0..1);

Pour cela nous remplaçons l'intégrande par son développement au voisinage de u=0. Cela revient à dire que les valeurs de la fonction en les points un peu éloignés du point qui donne le maximum peuvent être négligées.

> da:=series(1/sqrt(2*u-u^2),u);

Nous évacuons le terme d'erreur pour pouvoir calculer. Un traitement sérieux demanderait de le prendre en compte.

> da:=convert(da,polynom);

Ensuite nous intégrons le développement terme à terme. On note que nous prolongeons l'intégrale jusqu'à l'infini. Cette approximation va permettre d'obtenir des valeurs explicites, essentiellement parce que l'on fait apparaître la fonction gamma, définie comme d'habitude par la formule

.

On introduit donc une nouvelle erreur dont on pourrait montrer qu'elle est négligeable.

> assume(x>0):

> DA:=map(expr->int(expr*exp(-x*u),u=0..infinity),da);

On remet en place le facteur apparu au début, qui est la valeur maximale de la fonction intégrée.

> DA:=map(expr->exp(x)*expr,DA);

L'hypothèse faite sur la variable x lui a partiellement enlevé son statut d'indéterminée, c'est pourquoi on restaure ce statut en fin de calcul.

> x:='x':

La méthode que nous venons d'employer est la méthode de Laplace, qui est présentée pages 221-222. Elle fonctionne correctement parce que les termes d'erreur introduits sont exponentiellement petits par rapport aux termes du développement. Il est clair qu'il reste à justifier les calculs précédents.

Retour en haut de page

3. L'exemple suivant est assez similaire à celui que nous venons de traiter.

> F:=Int(exp(x*ln(1-t^2)),t=0..1);

Remarquons que l'intégrale existe bien car l'intégrale se prolonge par continuité en t=0. La fonction a un maximum à la borne.

> series(ln(1-t^2),t);

Comme dans l'exemple précédent nous procédons donc à un changement de variables. On notera que c'est la valeur prise à la borne qui dicte le changement de variables.

> G:=student[changevar](ln(1-t^2)=-u,F,u);

L'intégrande s'exprime comme le produit de exp(-x*u) par une fonction de u. C'est le comportement de cette fonction au voisinage de zéro qui détermine le comportement de l'intégrale. Nous calculons donc le développement de la fonction au voisinage de zéro.

> f:=remove(has,op(1,G),x);

> da:=series(f,u);

> da:=convert(da,polynom);

Ensuite nous intégrons le développement terme à terme. Comme dans le cas précédent, l'intervalle d'intégration est prolongé jusqu'à l'infini, ce qui est possible parce que la queue de la fonction intégrée est exponentiellement petite, à cause du terme exp(-x*u).

> assume(x>0):

> DA:=map(expr->int(expr*exp(-x*u),u=0..infinity),da);

Pour tester le résultat nous procédons à une petite expérience numérique.

> xx:=10:

> evalf(Int((1-t^2)^xx,t=0..1)),evalf(subs(x=xx,DA));

Tout paraît normal.

> x:='x':

Retour en haut de page

4. Passons à l'exemple suivant.

> F:=Int(exp(x*ln(ln(1+t))),t=0..1);

Le terme en facteur du x, dans l'exponentielle, varie de l'infini négatif à la valeur ln(ln(2)).

> plot(ln(ln(t+1)),t=0..1);

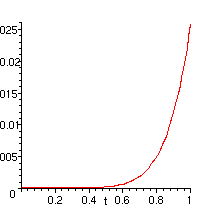
Du coup c'est le comportement en t=1 qui va donner le comportement de l'intégrale. En effet dès que t est en dessous de exp(1)-1 la fonction est écrasée à cause de l'exponentielle, et à droite de cette valeur elle reste exponentiellement petite par rapport à la valeur atteinte en t=1, comme on le voit ci-dessous.

> xx:=10:

> plot(exp(xx*ln(ln(t+1))),t=0..1);

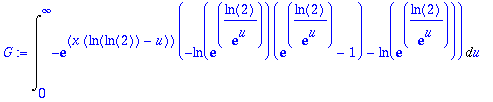
Comme dans les exemples précédents nous effectuons donc un changement de variables qui s'appuie sur la valeur maximale.

> G:=student[changevar](ln(ln(t+1))=ln(ln(2))-u,F,u);

Dans l'intégrale obtenue nous mettons en facteur le terme exp(x*ln(ln(2))), qui correspond à la valeur maximale. Ensuite nous procédons à l'étude locale de la fonction en facteur du exp(-x*u).

> f:=remove(has,op(1,G),x);

> da:=series(f,u,3);

> da:=convert(da,polynom):

Nous intégrons le développement terme à terme, toujours en prolongeant l'intervalle d'intégration jusqu'à l'infini.

> assume(x>0):

> DA:=map(expr->int(expr*exp(-x*u),u=0..infinity),da);

Nous réintroduisons le terme mis en facteur.

> DA:=map(expr->exp(x*ln(ln(2)))*expr,DA);

Nous obtenons ainsi un développement asymptotique de l'intégrale. Nous pouvons procéder à un petit test numérique.

> xx:=10:

> evalf(subs(x=xx,Int(exp(x*ln(ln(1+t))),t=0..1))),

    evalf(subs(x=xx,DA));

Tout va pour le mieux.

> x:='x':

Retour en haut de page

5. Dans l'exemple suivant la fonction en facteur du x dans l'exponentielle varie de manière monotone et atteint son maximum en t=Pi.

> F:=Int(sin(t)*exp(x*ln(t)),t=0..Pi);

Nous effectuons donc un changement de variables qui nous ramène à la forme standard, en tenant compte de cette valeur maximale.

> G:=student[changevar](ln(t)=ln(Pi)-u,F,u);

> expand(op(1,G));

Ensuite nous développons le cofacteur de l'exponentielle exp(-x*u) au voisinage de u=0.

> f:=remove(has,expand(op(1,G)),x);

> da:=series(f,u);

Puis nous intégrons terme à terme. Comme dans chaque exemple ceci suppose que la contribution au voisinage de u=0 est essentielle ; l'extension de l'intégrale jusqu'à l'infini crée une erreur négligeable.

> da:=convert(map(expand,da),polynom):

> assume(x>0):

> DA:=map(expr->int(expr*exp(-x*u),u=0..infinity),da);

Nous obtenons ainsi le développement cherché.

> DA:=Pi^x*map(collect,DA,[x,Pi]);

Procédons à un test numérique.

> xx:=12:

> evalf(subs(x=xx,Int(sin(t)*exp(x*ln(t)),t=0..Pi))),

  evalf(subs(x=xx,DA));

Le résultat n'est pas mirifique. Évacuons le Pi^x (le terme d'erreur ne donne qu'une erreur relative, et non une erreur absolue) et regardons les valeurs des termes du développement.

> Da:=DA/Pi^x:

> for k from -degree(Da,x) to -ldegree(Da,x) do

    Termf[k]:=evalf(subs(x=xx,select(has,Da,x^(-k))))

  od;

Les termes ont l'air de décroître en valeur absolue. Il faudrait aller plus loin. Augmentons donc la précision des calculs.

> Order:=40:

> da:=series(f,u):

> da:=convert(map(expand,da),polynom):

> Da:=map(expr->int(expr*exp(-x*u),u=0..infinity),da):

> Da:=map(collect,Da,[x,Pi]):

> r:=-degree(Da,x)..-ldegree(Da,x);

> for k from op(1,r) to op(2,r) do

    Termf[k]:=evalf(subs(x=xx,select(has,Da,x^(-k))))

  od:

  k:='k':

> plot([seq([i,abs(Termf[i])],i=r)]);

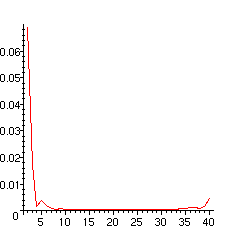
La valeur absolue des termes du développement décroît au début puis se met à croître. Regardons de plus près.

> r1:=8..35:

> plot([seq([i,abs(Termf[i])],i=r1)]);

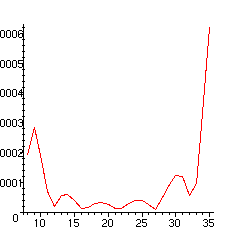
Dans ce type de problème, on s'attend à ce que le terme en x^(-n) du développement ait un coefficient de l'ordre de n!. Si l'on fixe la valeur de x, les termes du développement vont d'abord décroître, puis ensuite croître en valeur absolue et la série asymptotique sera divergente. Le changement de comportement a lieu pour n de l'orde de x. C'est ce que l'on observe ici. Dans ces conditions on obtient une assez bonne approximation en sommant au plus petit terme (c'est une expression consacrée). Ici est le phénomène est un peu flou, car la valeur absolue des termes fluctue avant d'exploser. On peut cependant constater que l'on obtient d'assez bonnes approximations en sommant dans l'intervalle où les termes restent petits.

> exact:=evalf(subs(x=xx,Int(sin(t)*exp(x*ln(t)),t=0..Pi)/Pi^x));

> plot([[seq([j,add(Termf[i],i=op(1,r)..j)],j=r)],

              [seq([j,exact],j=r)]],color=[red,blue]);

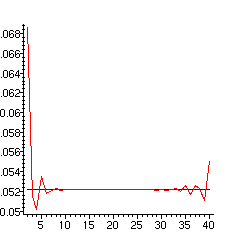
> plot([[seq([j,add(Termf[i],i=op(1,r)..j)],j=r1)],

             [seq([j,exact],j=r1)]],color=[red,blue]);

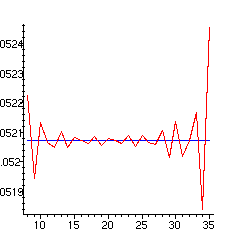
Il faut aussi noter que la question est assez subtile puisqu'on emploie un développement asymptotique, valable pour x très grand, pour mener un calcul numérique, pour x seulement un peu grand.

> x:='x':

> Order:=6:

L'approche précédente a le mérite d'être méthodique. On peut aussi essayer d'être astucieux et ceci va nous permettre de trouver la forme des coefficients du développement que nous venons d'obtenir. Une première idée qui vient pour mettre en valeur le fait que la contribution dominante dans l'intégrale vient du voisinage de Pi consiste à opérer le changement de variables suivant.

> H:=student[changevar](t=Pi*(1-s),F,s);

> H:=expand(H);

On a ensuite envie de développer le sinus au voisnage de zéro et d'intégrer terme à terme.

> h:=op(1,select(has,H,{int,Int}));

> da1:=series(sin(Pi*s),s);

> da1:=convert(da1,polynom):

Les intégrales des s^k*(1-s)^x sont des intégrales Bêta, des valeurs de l'intégrale eulérienne de première espèce, qui sont connues.

> assume(x>0):

> DA1:=Pi^x*map(expr->Pi*int(expr*(1-s)^x,s=0..1),da1);

On arrive ainsi au développement suivant pour l'int'egrale proposée,

.

Il faut noter que ce développement est convergent, contrairement au développement que nous avons déjà obtenu. D'autre part c'est aussi un développement asymptotique, mais par rapport à une échelle différente de l'échelle usuelle. On a ce que l'on appelle une série de faculté (Fakultätenreihen, faculty series, [Knopp90, pp. 446-448]). Enfin il faut noter que si l'on développe brutalement les termes de ce nouveau développement dans l'échelle usuelle, on fait réapparaître le développement déjà obtenu.

> asympt(DA1,x);

Une deuxième façon de procéder consiste à reprendre la fonction que nous avons utilisée au début en la développant suivant les puissances de exp(-u), au lieu de la développer suivant les puissances de u.

> Order:=8:

> f;

> da2:=series(subs(exp(u)=1/v,f),v);

> da2:=combine(subs(v=exp(-u),convert(da2,polynom)),power);

Cette manière de développer est correcte car on emploie une série entière de rayon de convergence infini. De plus l'exponentielle de -u reste dans un segment et on peut donc intégrer terme à terme.

> DA2:=Pi^x*map(expr->int(expr*exp(-x*u),u=0..infinity),da2);

On obtient ainsi un nouveau développement, qui comme le précédent est convergeant,

.

Par contre on ne peut pas le voir comme un développement asymptotique. Si nous développons chaque terme de la série de la manière suivante,

et si nous échangeons sans scrupule les signes de sommation, nous obtenons le développememt suivant

.

La manoeuvre est peu soigneuse, mais nous remarquons que nous savons sommer chacun des coefficients du développement en x ci-dessus. Si nous effectuons les premières sommations,

> for mm from 0 to 5 do

    collect(sum((-1)^(k+1)*Pi^(2*k)*(2*k)^mm/(2*k)!,

                                      k=1..infinity),Pi)

  od;

nous retrouvons les coefficients que nous avons déjà rencontré. Nous avons donc deviné une expression explicite des coefficients du développement asymptotique cherché. Pour être plus précis, il faudrait développer le (2*k)^m suivant les factorielles descendantes, ce qui ferait apparaître les nombres de Stirling de seconde espèce [Comtet70, tome second, chap. 2]. D'ailleurs une petite expérience met clairement en valeur les nombres de Stirling.

> for mm from 0 to 5 do

    collect(sum((-1)^(k+1)*z^(2*k)*(2*k)^mm/(2*k)!,

                                     k=1..infinity),z)

  od;

> for mm from 0 to 5 do

    seq(combinat[stirling2](mm,kk),kk=0..mm)

  od;

Retour en haut de page

6. Ce dernier exemple est légèrement différent des précédents parce que la fonction en facteur du x dans l'exponentielle n'atteint pas son maximum en une borne de l'intervalle.

Clairement le maximum de -t^2 est atteint en zéro. Si l'on voulait procéder comme dans les exemples 2 à 4, il faudrait couper l'intégrale en deux, au point 0 et poser dans chacune des deux intégrales t^2=u. Ici on peut se contenter de travailler directement avec la forme fournie par l'énoncé.

> F:=Int(exp(-x*t^2)*sqrt(1+t^2),t=-infinity..infinity);

Nous développons le cofacteur de l'exponentielle au voisinage du point critique 0 et nous intégrons le développement terme à terme, en prolongeant l'intervalle d'intégration jusqu'à l'infini.

> f:=remove(has,op(1,F),x);

> da:=series(f,t);

> da:=convert(da,polynom):

> assume(x>0):

> DA:=map(expr->int(expr*exp(-x*t^2),

                                     t=-infinity..infinity),da);

Le test numérique qui suit nous satisfait.

> xx:=10:

> evalf(subs(x=xx,Int(exp(-x*t^2)*sqrt(1+t^2),

                                        t=-infinity..infinity))),

  evalf(subs(x=xx,DA));

Bien sûr, nous n'avons pas dans ce qui précède fourni de preuves qui valident les développements obtenus. Par contre les calculs mettent bien en valeur les idées de la méthode de Laplace. Pour en savoir plus on peut consulter [DeBruijn81,ch. 4] ou [Dieudonne80,sect. IV.2]. On peut aussi s'appuyer sur l'excellent [Olver74].

Retour en haut de page

Retour en page principale