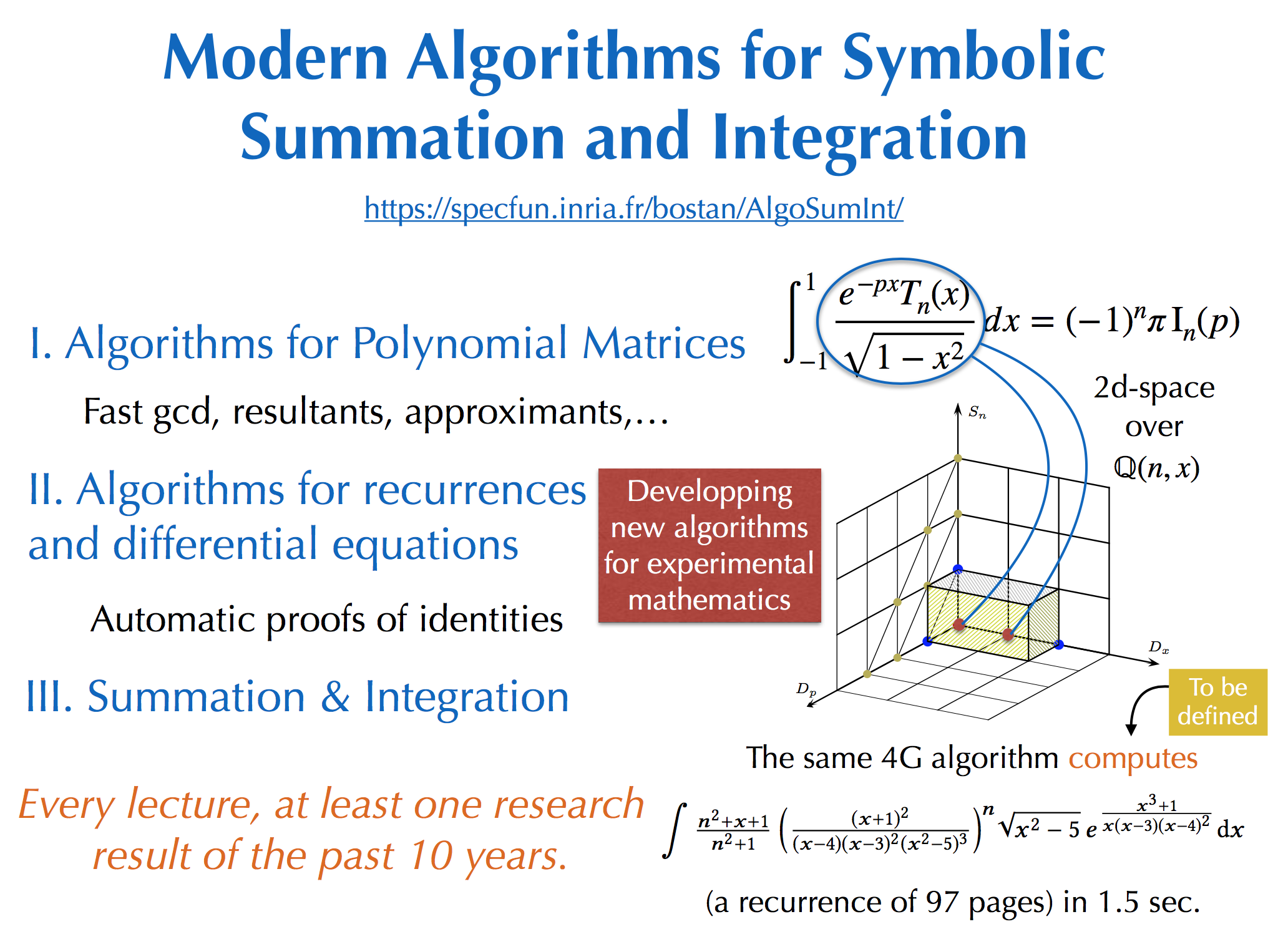
Context: The course "Modern Algorithms for Symbolic Summation and Integration" is a research course from the Master 2 in Computer Science program, of the Computer Science Department of the Ecole Normale Supérieure in Lyon.
The lectures will be delivered in the academic year 2022-2023 (for 16 x 2h and 5 ECTS), on Wednesdays (3:45pm-5:45pm) and Thursdays (8am-10am), during the period 14/09/2022 and 10/11/2022 (see the detailed schedule below).

Instructors: Alin Bostan, Bruno Salvy, Gilles Villard.

Description: Computer Algebra, or Symbolic Computation, consists of representing and manipulating mathematical objects on a computer in an exact way, in contrast with the traditional scientific computing. In this course, we present a very active research topic in Computer Algebra – the development of algorithms for symbolic summation and symbolic integration. The emergence of these algorithms has put an important family of computational tools in the hands of discrete mathematicians, and many results that were inaccessible in other ways have been found and proved by computer methods. These algorithms are also nowadays unavoidable in physics, for the numerical evaluation of special functions, and more broadly for the difficult questions of simplification of formulas.

Prerequisites: Preferably the audience should have followed a level M1 introductory course in Computer Algebra. In particular, notions on basic algebraic objects (polynomials, matrices, power series) and basic algebraic algorithms (Gaussian elimination, Euclidean algorithm) will be helpful.

Objective: We will explain, among other things, how modern computer algebra answers the following open problem from the book The Art of Computer Programming, Volume 1: Fundamental Algorithms by Donald E. Knuth, Addison Wesley, Reading, Massachusetts, 1968:
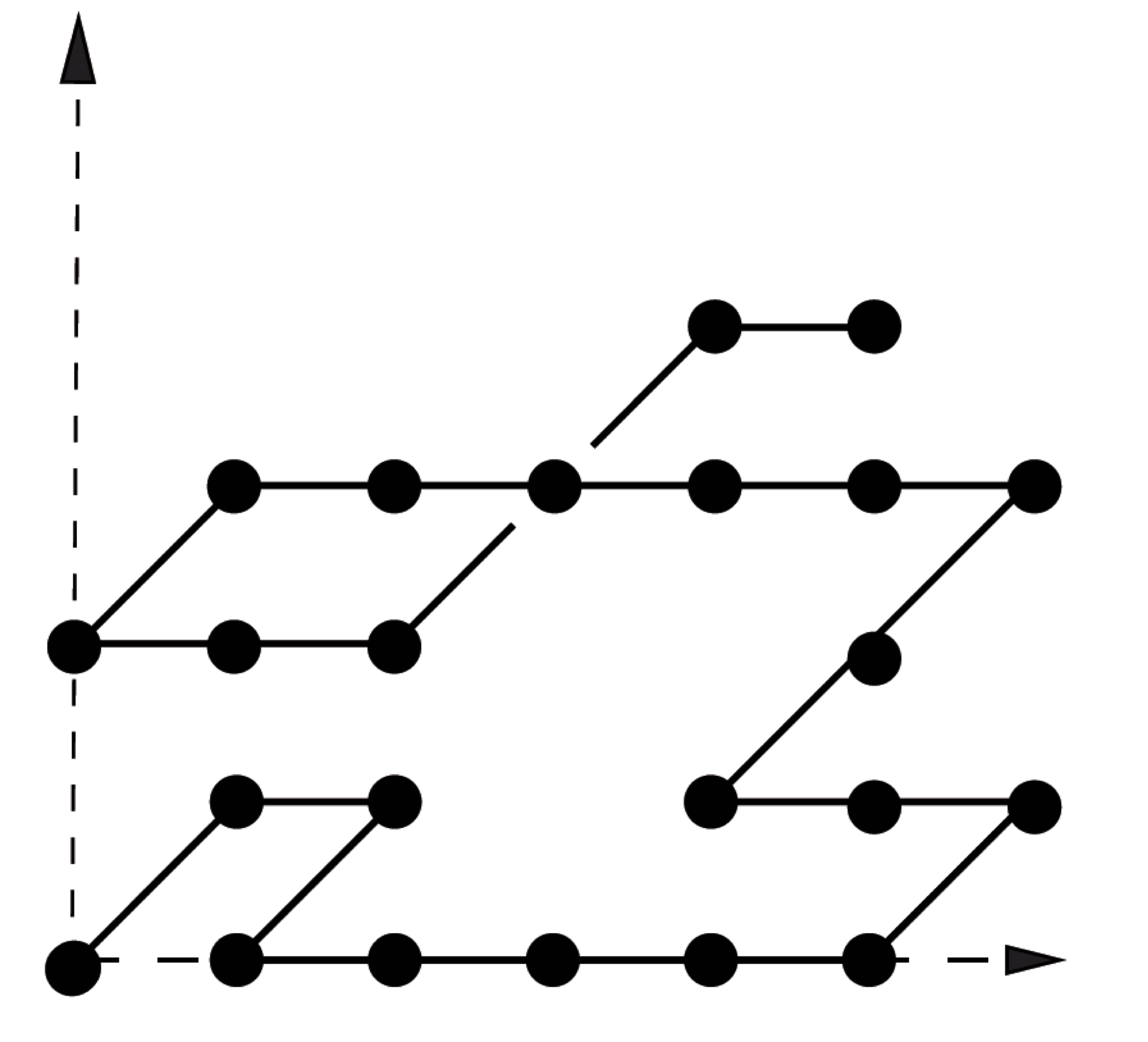
[50] Develop computer programs for simplifying sums that involve binomial coefficients. As an example of a recent combinatorial application of the algorithms presented in this course, we will describe a computer-driven proof of the following fact: the counting generating function of walks with prescribed length, with allowed steps in the set X, starting from the origin and confined to the quarter plane is:
• algebraic if X = {E, W, NE, SW} (Gessel walks, see figure below);
• transcendental if X = {N, S, NE, NW} (trident walks).

Detailed plan of the lectures:

Wednesdays (3:45pm-5:45pm) and Thursdays (8am-10am)

Material for the course (slides, demos, exercises, etc.)

• 0- Introduction (Wed 7/9/2022 and Thu 8/9/2022, Bruno Salvy).
• 1- Algorithms for polynomial matrices.
  • Matrix and polynomial computations (Wed 14/9/2022, Gilles Villard).
  • Padé-Hermite approximation (Thu 15/9/2022, Gilles Villard).
  • Alternative to Gaussian elimination (Wed 21/9/2022, Gilles Villard).
  • Exercises session (Thu 22/9/2022, Gilles Villard).
  • Fast bivariate resultants and composition (Thu 13/10/2022, Gilles Villard).
• 2- Algorithms for recurrence and differential equations.
  • Fast skew arithmetic (Wed 28/9/2022, Alin Bostan).
  • Algorithmic guessing of algebraic and differential equations (Thu 29/9/2022, Alin Bostan).
  • Polynomial, rational and hypergeometric solutions of linear differential/recurrence equations (Wed 5/10/2022, Alin Bostan).
  • Exercises session (Thu 6/10/2022, Alin Bostan).
• 3- Algorithms for symbolic summation and integration.
  • Creative Telescoping — from 1G to 4G algorithms (Wed 19/10/2022, Alin Bostan).
  • Definite integration of multivariate rational functions (Thu 20/10/2022, Bruno Salvy).
  • Multiple binomial sums (Wed 26/10/2022, Bruno Salvy).
  • Combinatorial applications (Wed 9/11/2022, Alin Bostan).
  • Definite integration of general D-finite functions (Thu 27/10/2022, Bruno Salvy).

Validation: There will be a mid-term exam (We 12/10/2022) and a written final exam (Thu 10/11/2022).

Bibliography:

ARTICLES (click on the title to get the pdf):
• G. Villard: On computing the resultant of generic bivariate polynomials. ISSAC'18, 391‐398, ACM Press, 2018.
• W. Zhou, G. Labahn: Efficient algorithms for order basis computation. J. Symbolic Comput. 47 (2012), no. 7, 793‐819.
• A. Storjohann: High-order lifting and integrality certification. J. Symbolic Comput. 36 (2003), no. 3-4, 613‐648.
• W. Zhou, G. Labahn, A. Storjohann: A deterministic algorithm for inverting a polynomial matrix. J. Complexity 31 (2015), no. 2, 162‐173.
• G. Labahn, V. Neiger, W. Zhou: Fast, deterministic computation of the Hermite normal form and determinant of a polynomial matrix. J. Complexity 42 (2017), 44‐71.

• A. Benoit, A. Bostan, J. van der Hoeven: Quasi-optimal multiplication of linear differential operators. FOCS 2012, 524‐530, IEEE Computer Soc., 2012.
• A. Bostan, F. Chyzak, Z. Li, B. Salvy: Fast computation of common left multiples of linear ordinary differential operators. ISSAC'12, 99‐106, ACM Press, 2012.
• J. van der Hoeven: On the complexity of skew arithmetic. Appl. Algebra Engrg. Comm. Comput. 27 (2016), no. 2, 105‐122.
• A. Bostan, T. Cluzeau, B. Salvy: Fast algorithms for polynomial solutions of linear differential equations. ISSAC'05, 45‐52, ACM Press, 2005.
• A. Bostan, F. Chyzak, T. Cluzeau, B. Salvy: Low complexity algorithms for linear recurrences. ISSAC'06, 31‐38, ACM Press, 2006.

• F. Chyzak: An extension of Zeilberger's fast algorithm to general holonomic functions. Discrete Math. 217 (2000), no. 1-3, 115‐134.
• A. Bostan, S. Chen, F. Chyzak, Z. Li: Complexity of Creative Telescoping for Bivariate Rational Functions. ISSAC'10, pp. 203‐210, ACM Press, 2010.
• A. Bostan, P. Lairez, B. Salvy: Creative telescoping for rational functions using the Griffiths-Dwork method. ISSAC'13, pp. 93‐100, ACM Press, 2013.
• A. Bostan, P. Lairez, B. Salvy: Multiple binomial sums. J. Symbolic Comput. 80 (2017), part 2, 351‐386.
• A. Bostan, F. Chyzak, P. Lairez, B. Salvy: Generalized Hermite Reduction, Creative Telescoping and Definite Integration of D-Finite Functions. ISSAC'18, pp. 95‐102, ACM Press, 2018.


BOOKS (click on the title to go to the book's website and on the image to get the pdf):
• M. Petkovsek, W. Wilf, D. Zeilberger, A=B, A. K. Peters, 1996.
• A. Bostan, F. Chyzak, M. Giusti, R. Lebreton, G. Lecerf, B. Salvy, É. Schost, Algorithmes Efficaces en Calcul Formel, CreateSpace, 2017.
• J. von zur Gathen, J. Gerhard, Modern Computer Algebra, Cambridge University Press, 1999.